题目内容
13.求证:f(x)=x+$\frac{1}{x}$,在(0,1)单调递减,在(1,+∞)单调递增.分析 先求出函数的导数,通过x的范围,确定导函数的符号,从而得出函数的单调性.
解答 证明:∵f(x)=x+$\frac{1}{x}$,
∴f′(x)=1-$\frac{1}{{x}^{2}}$,
当x∈(0,1)时,
f′(x)=1-$\frac{1}{{x}^{2}}$<0,
∴f(x)=x+$\frac{1}{x}$在(0,1)上单调递减,
当x∈(1,+∞)时,
f′(x)=1-$\frac{1}{{x}^{2}}$>0,
∴f(x)=x+$\frac{1}{x}$在(1,+∞)上单调递增.
点评 本题考查了函数的单调性问题,考查了分类讨论思想,是一道基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
3.a=6,c=1的椭圆的标准方程是( )
| A. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{35}$ | B. | $\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{35}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{5}$=1 | D. | 以上都不对 |
1.执行如图所示的程序框图(算法流程图),当输出的S的值为-10时,S0的值是( )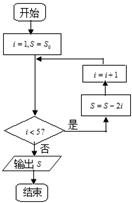

| A. | 6 | B. | 8 | C. | 12 | D. | 10 |
8.若集合M={y|y=2x,x∈R},N={x|y=lg(x-1)},则下列各式中正确的是( )
| A. | M∪N=M | B. | M∪N=N | C. | M=N | D. | M∩N=∅ |
3.有两个分类变量X与Y,其一组观测值的2×2列联表如下表,其中a,10-a均为大于1的整数,若K2观测值k>2,则a的取值为( )
| Y1 | Y2 | |
| X1 | 5+a | 15-a |
| Y1 | 10-a | 20-a |
| A. | 6或7 | B. | 7 | C. | 8 | D. | 7或8 |