题目内容
18.已知函数f(x)=x2-2(a-1)x+2,x∈[-5,5].(1)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数;
(2)求f(x)最小值.
分析 (1)通过配方可知函数y=f(x)的图象是以x=a-1为对称轴、开口向上的抛物线,进而可得结论;
(2)通过(1)、分对称轴在区间[-5,5]的左侧、中间、右侧三种情况讨论即可.
解答 解:(1)f(x)=x2-2(a-1)x+2
=[x-(a-1)]2+2-(a-1)2
=[x-(a-1)]2+1+2a-a2,
∴当a-1≤-5或a-1≥5即a≤-4或a≥6时y=f(x)在区间[-5,5]上是单调函数;
(2)通过(1)可知,当a≤-4时,y=f(x)在区间[-5,5]上单调递增,
∴f(x)min=f(-5)=25+10a-10+2=10a+17;
当a≥6时,y=f(x)在区间[-5,5]上单调递减,
∴f(x)min=f(5)=25-10a+10+2=-10a+37;
当-4<a<6时,y=f(x)在区间[-5,a-1)上单调递减,在区间[a-1,5]上单调递增,
∴f(x)min=f(a-1)=1+2a-a2;
综上所述,f(x)min=$\left\{\begin{array}{l}{10a+17,}&{a≤-4}\\{1+2a-{a}^{2},}&{-4<a<6}\\{-10a+37,}&{a≥6}\end{array}\right.$.
点评 本题考查二次函数的性质,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
8.已知抛物线C:y2=2px(p>0)的焦点F(1,0),若点P在抛物线C上运动,点Q在直线x+y+5=0上运动,则|PQ|的最小值为( )
| A. | $\frac{9\sqrt{2}}{4}$ | B. | $\frac{19\sqrt{2}}{8}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
9.若a>b>0>c,则以下不等式恒成立的是( )
| A. | $\frac{1}{a}$+$\frac{1}{b}$>$\frac{1}{ab}$ | B. | $\frac{c}{a-c}$>$\frac{c}{b-c}$ | C. | ac>bc | D. | a2+b2>c2 |
3.某位同学设计下面的程序框图用以计算和式12+22+32+…+212的值,则在判断框中应填写( )


| A. | i≤20 | B. | i≥20 | C. | i≤22 | D. | i≤21 |
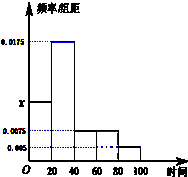 某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]
某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]