题目内容
3．a=6，c=1的椭圆的标准方程是（ ）| A． | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{35}$ | B． | $\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{35}$=1 | C． | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{5}$=1 | D． | 以上都不对 |
分析 由已知求得b，然后需分焦点在x轴和y轴求取椭圆的标准方程．
解答 解：由a=6，c=1，得b2=a2-c2=36-1=35，
∴所求椭圆的标准方程为：$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{35}=1$或$\frac{{y}^{2}}{36}+\frac{{x}^{2}}{35}=1$．
故选：D．
点评 本题考查椭圆方程的求法，解答此题要分焦点在不同的坐标轴上，是基础题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
13．已知a为如图所示的算法框图中输出的结果，则二项式${（x+\frac{a}{x^2}）^9}$的展开式中的常数项为（ ）
| A． | 84 | B． | -84 | C． | 672 | D． | -672 |
已知椭圆C1：$\frac{x^2}{4}+{y^2}$=1的左、右焦点分别是F1、F2，Q是椭圆外的动点，满足|$\overrightarrow{{F_1}Q}$|=4．点P是线段F1Q与该椭圆C1的交点，点T在线段F2Q上，并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0，|$\overrightarrow{T{F}_{2}}$|≠0．
18．如图所示的是一串黑白相间排列的珠子，若按这种规律排列下去，那么第34颗珠子的颜色是（ ）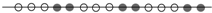
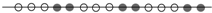
| A． | 白色 | B． | 白色的可能性大 | C． | 黑色 | D． | 黑色的可能性大 |
8．已知抛物线C：y2=2px（p＞0）的焦点F（1，0），若点P在抛物线C上运动，点Q在直线x+y+5=0上运动，则|PQ|的最小值为（ ）
| A． | $\frac{9\sqrt{2}}{4}$ | B． | $\frac{19\sqrt{2}}{8}$ | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
