题目内容
16.若圆心在x轴上的圆C同时经过椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F,上顶点B和右顶点A,则椭圆Γ的离心率为$\frac{\sqrt{5}-1}{2}$.分析 求出圆的圆心与椭圆的上顶点的距离等于圆的半径,然后求出椭圆的离心率即可.
解答 解:由题意可知圆的圆心坐标为($\frac{a-c}{2}$,0),椭圆的上顶点(0,b),
所以($\frac{a-c}{2}$)2+b2=($\frac{a+c}{2}$)2,
即b2=ac,又b2=a2-c2,所以a2-c2-ac=0,即e2+e-1=0,解得e=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查椭圆的基本性质的应用,椭圆的离心率的求法,圆与椭圆的位置关系,考查计算能力.

练习册系列答案
相关题目
11.若某空间几何体的三视图如图所示,则该几何体的体积为( )
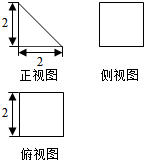

| A. | $\frac{8}{3}$ | B. | 8 | C. | 4 | D. | $\frac{4}{3}$ |