题目内容
6．某社区要为小凯等4名志愿者和他们帮助的2位老人拍照，要求这6人排成一排，小凯必须与2位老人都相邻，且2位老人不排在两端，则不同的排法种数是（ ）| A． | 12 | B． | 24 | C． | 36 | D． | 48 |
分析 小凯必须与2位老人都相邻，用捆绑法，有A22=2，两位老人不排在两端，则小凯与2位老人在2、3、4或3、4、5位置，其余有A33=6，利用乘法原理即可得出结论．
解答 解：小凯必须与2位老人都相邻，用捆绑法，有A22=2，两位老人不排在两端，则小凯与2位老人在2、3、4或3、4、5位置，其余有A33=6，故共有2×2×6=24种，
故选：B．
点评 本题考查排列、组合的实际应用，考查学生分析解决问题的能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．设函数y=$\sqrt{x+1}$的定义域为M，已知全集U=R，集合N={x|0＜x≤2}，则M∩∁UN=（ ）
| A． | {x|-1≤x＜0或x≥2} | B． | {x|-1≤x≤0或x≥2} | C． | {x|-1≤x≤0或x＞2} | D． | {x|0≤x＜2} |
11．若集合A={x|x＞-1}，B={x|-2＜x＜3}，则A∩B=（ ）
| A． | {x|x＞-1} | B． | {x|-1＜x＜3} | C． | {x|x＞-2} | D． | {x|-2＜x＜3} |
18．
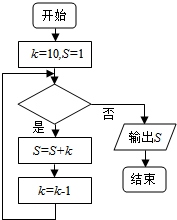若如框图所给的程序运行结果为S=28，那么判断框中应填入的条件是（ ）
若如框图所给的程序运行结果为S=28，那么判断框中应填入的条件是（ ）| A． | k＜7？ | B． | k≤7？ | C． | k＞7？ | D． | k≥7？ |