题目内容
7.在△ABC中,若D为BC 的中点,则有$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,将此结论类比到四面体中,在四面体 A-BCD中,若G为△BCD的重心,则可得一个类比结论:$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})$.分析 “在△ABC中,D为BC的中点,则有$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,平面可类比到空间就是“△ABC”类比“四面体A-BCD”,“中点”类比“重心”,可得结论.
解答 解:由“△ABC”类比“四面体A-BCD”,“中点”类比“重心”有,
由类比可得在四面体A-BCD中,G为△BCD的重心,则有$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})$.
故答案为:$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})$.
点评 本题考查了从平面类比到空间,属于基本类比推理.利用类比推理可以得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
18.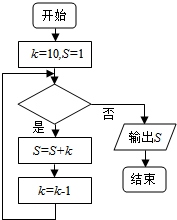 若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
 若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )| A. | k<7? | B. | k≤7? | C. | k>7? | D. | k≥7? |