题目内容
8.某班有50名学生,一次考试后数学成绩X~N(110,σ2),若P(100≤X≤110)=0.3,则估计该班学生数学成绩在120分以上的人数为( )| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
分析 根据考试的成绩X服从正态分布N(110,σ2),得到考试的成绩X关于X=110对称,根据P(100≤X≤110)=0.3,得到P(X≥120)=0.2,根据频率乘以样本容量得到这个分数段上的人数.
解答 解:∵考试的成绩X服从正态分布N(110,σ2).
∴考试的成绩X关于X=110对称,
∵P(100≤X≤110)=0.3,
∴P(X≥120)=P(X≤100)=$\frac{1}{2}$(1-0.3×2)=0.2,
∴该班数学成绩在120分以上的人数为0.2×50=10.
故选:A.
点评 本题考查正态曲线的特点及曲线所表示的意义,是一个基础题,解题的关键是考试的成绩X关于X=110对称,利用对称写出要用的一段分数的频数,题目得解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.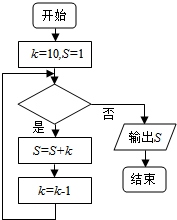 若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
 若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )| A. | k<7? | B. | k≤7? | C. | k>7? | D. | k≥7? |