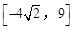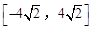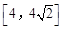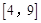题目内容
已知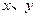 为正实数,且满足关系式
为正实数,且满足关系式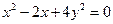 ,求
,求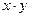 的最大值.
的最大值.
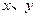 为正实数,且满足关系式
为正实数,且满足关系式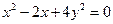 ,求
,求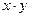 的最大值.
的最大值.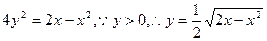 ,
,∴
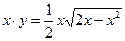 .
.由
 解得
解得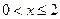 .
.设

当
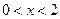 时,
时,
 .
.令
 ,得
,得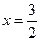 或
或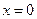 (舍).
(舍).∴
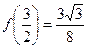 ,又
,又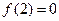 ,∴函数
,∴函数 的最大值为
的最大值为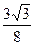 .
.即
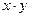 的最大值为
的最大值为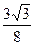 .
.题中有两个变量x和y,首先应选择一个主要变量,将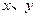 表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值
表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值
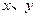 表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值
表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值
练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
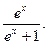
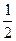 )对称;
)对称;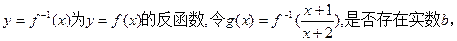 使得任给
使得任给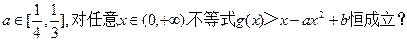 若存在,求b的取值范围;若不存在,说明理由.
若存在,求b的取值范围;若不存在,说明理由.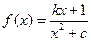 (
(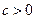 且
且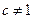 ,
,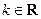 )恰有一个极大值点和一个极小值点,其中一个是
)恰有一个极大值点和一个极小值点,其中一个是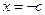 .
.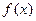 的另一个极值点;
的另一个极值点;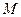 和极小值
和极小值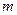 ,并求
,并求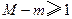 时
时 的取值范围.
的取值范围.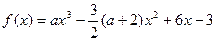
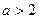 时,求函数
时,求函数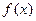 的极小值
的极小值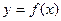 与
与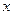 轴的公共点的个数。
轴的公共点的个数。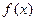 =
=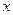 (1-
(1-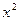 )在[0,1]上的最大值为__________.
)在[0,1]上的最大值为__________.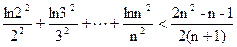 (n∈N
(n∈N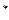 ,n≥2)
,n≥2) ,则函数
,则函数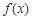 在区间
在区间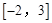 上的值域是( )
上的值域是( )