题目内容
设函数f(x)=lnx-px+1
(1)当P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围
(2)证明: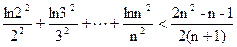 (n∈N
(n∈N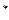 ,n≥2)
,n≥2)
(1)当P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围
(2)证明:
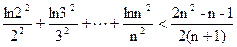 (n∈N
(n∈N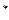 ,n≥2)
,n≥2)(1)P≥1 (2)证明如下
(1)f(x)=ln2x-px+1定义域(0,+∞),f′(x)=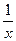 -p=
-p=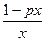 =
=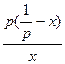
当P>0时,令f′(x)=0,x=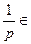 (0,+∞)
(0,+∞)
当x∈(0,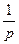 )时,f′(x)>0 f(x)为增函数,
)时,f′(x)>0 f(x)为增函数,
当x∈(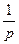 ,+∞)时f′(x)<0
,+∞)时f′(x)<0
f(x)为减函数。
f(x)max=f(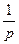 )=ln
)=ln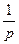
要使f(x)≤0恒成立只要f(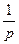 )=ln
)=ln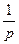 ≤0
≤0
∴P≥1
(2)令P="1" 由(1)知:lnx-x+1≤0
∴lnx≤x-1 n≥2
lnn2≤n2-1
∴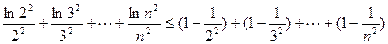
=(n-1)-(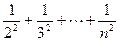 )
)
<(n-1)-[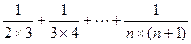 ]
]
=(n-1)-(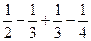 +
+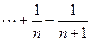 )
)
=(n-1)-( )
)
=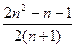
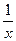 -p=
-p=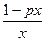 =
=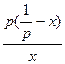
当P>0时,令f′(x)=0,x=
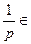 (0,+∞)
(0,+∞)当x∈(0,
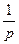 )时,f′(x)>0 f(x)为增函数,
)时,f′(x)>0 f(x)为增函数,当x∈(
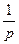 ,+∞)时f′(x)<0
,+∞)时f′(x)<0f(x)为减函数。
f(x)max=f(
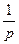 )=ln
)=ln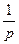
要使f(x)≤0恒成立只要f(
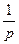 )=ln
)=ln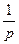 ≤0
≤0∴P≥1
(2)令P="1" 由(1)知:lnx-x+1≤0
∴lnx≤x-1 n≥2
lnn2≤n2-1

∴
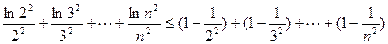
=(n-1)-(
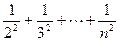 )
)<(n-1)-[
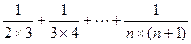 ]
]=(n-1)-(
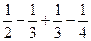 +
+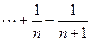 )
)=(n-1)-(
 )
)=
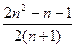

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
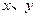 为正实数,且满足关系式
为正实数,且满足关系式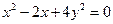 ,求
,求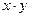 的最大值.
的最大值. 在区间
在区间 上的最大值是
上的最大值是
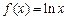 (Ⅰ)求函数
(Ⅰ)求函数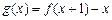 的最大值;(Ⅱ)当
的最大值;(Ⅱ)当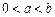 时,求证:
时,求证: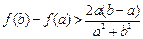 .
. ,
, 的最大值和最小值。
的最大值和最小值。 的最小值为( )
的最小值为( )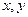 满足
满足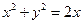 ,求
,求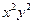 的取值范围。
的取值范围。