题目内容
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线
,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线 ![]() 相切.
相切.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点F1、斜率为k1的直线l1与椭圆E交于A,B两点,过点F2、斜率为k2的直线l2与椭圆E交于C,D两点,且直线l1 , l2相交于点P,若直线OA,OB,OC,OD的斜率kOA , kOB , kOC , kOD满足kOA+kOB=kOC+kOD , 求证:动点P在定椭圆上,并求出此椭圆方程.
【答案】解:(Ⅰ)由以椭圆短轴为直径的圆与直线 ![]() 相切,则圆心O到直线的距离d=b,
相切,则圆心O到直线的距离d=b,
∴b=d= ![]() =
= ![]()
由e= ![]() =
= ![]() ,则a=2c,
,则a=2c,
a2=c2+b2=c2+3,解得:a=2,c=1,
∴椭圆E的方程 ![]()
(Ⅱ)当直线l1或l2斜率不存在时,P点坐标为(﹣1,0)或(1,0).
当直线l1、l2斜率存在时,l1的方程为y=k1(x+1),l2的方程为y=k2(x﹣1),
设A(x1 , y1),B(x2 , y2),C(x3 , y3),D(x4 , y4),
联立 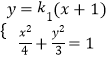 ,得到(3+4k12)x2+8k12x+4k12﹣12=0,
,得到(3+4k12)x2+8k12x+4k12﹣12=0,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() .
.
同理x3+x4= ![]() ,x3x4=
,x3x4= ![]() .(*)
.(*)
∵kOA= ![]() ,kOB=
,kOB= ![]() ,kOA+kOB=
,kOA+kOB= ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
同理可得:kOC+kOD= ![]() .
.
由kOA+kOB=kOC+kOD , 则 ![]() =
= ![]() .
.
整理得:k1k2=﹣3.
设点P(x,y),则 ![]()
![]() =﹣3,(x≠±1)
=﹣3,(x≠±1)
整理得: ![]() ,(x≠±1)
,(x≠±1)
由当直线l1或l2斜率不存在时,P点坐标为(﹣1,0)或(1,0)也满足,
∴椭圆的标准方程: ![]()
【解析】(Ⅰ)利用点到直线的距离公式,即可求得b,利用椭圆的离心率及a2=c2+b2 , 即可求得a的值,即可求得椭圆方程;(Ⅱ)当直线l1或l2斜率不存在时,求得P点坐标,当直线l1、l2斜率存在时,可得l1的方程为y=k1(x+1),l2的方程为y=k2(x﹣1).与椭圆方程联立即可得出根与系数的关系,再利用斜率计算公式和已知即可得出k1与k2的关系,利用直线的斜率,即可求得椭圆方程.

 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】某校期中考试后,按照学生的数学考试成绩优秀和不优秀进行统计,得到如下列联表:
优秀 | 不优秀 | 总计 | |
文科 | 60 | 140 | 200 |
理科 | 265 | 335 | 600 |
总计 | 325 | 475 | 800 |
(1)画出列联表的等高条形图,并通过图形判断数学成绩与文理分科是否有关;
(2)利用独立性检验,分析文理分科对学生的数学成绩是否有影响.
