Question

【题目】如图，在正方体ABCD﹣A1B1C1D1中，E为DD1的中点．求证：

（1）BD1∥平面EAC；
（2）平面EAC⊥平面AB1C．

Answer 1

【答案】
（1）证明：连接BD，交AC于O．连接EO，BD1．

因为E为DD1的中点，所以BD1∥OE．）

又OE平面EAC，BD1平面EAC，

所以BD1∥平面EAC

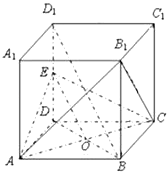
（2）证明：∵BB1⊥AC，BD⊥AC．BB1∩BD=B，BB1、BD在面BB1D1D 内

∴AC⊥平面BB1D1D

又BD1平面BB1D1D∴BD1⊥AC．

同理BD1⊥AB1，∴BD1⊥平面AB1C．

由（1）得BD1∥OE，∴EO⊥平面AB1C．

又EO平面EAC，∴平面EAC⊥平面AB1C

【解析】（1）连接BD，交AC于O．连接EO，BD1 ． 根据中位线可知BD1∥OE，又OE平面EAC，BD1平面EAC，根据线面平行的判定定理可知BD1∥平面EAC；（2）根据BB1⊥AC，BD⊥AC，BB1∩BD=B，满足线面垂直的判定定理，则AC⊥平面BB1D1D，又BD1平面BB1D1D则BD1⊥AC，同理BD1⊥AB1 ， 从而BD1⊥平面AB1C．根据（1）可得BD1∥OE，从而EO⊥平面AB1C，又EO平面EAC，根据面面垂直的判定定理可知平面EAC⊥平面AB1C．
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的性质是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．