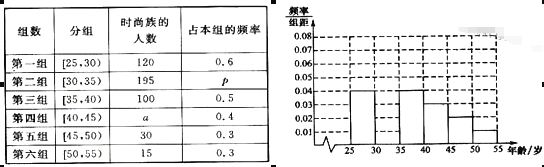
题目内容
【题目】已知函数f(x)=|2x﹣1|+|x+1|.
(1)求函数f(x)的值域M;
(2)若a∈M,试比较|a﹣1|+|a+1|, ![]() ,
, ![]() 的大小.
的大小.
【答案】
(1)解: 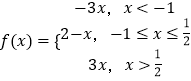 ,
,
根据函数f(x)的单调性可知,
当 ![]() 时,
时, ![]() .
.
所以函数f(x)的值域 ![]()
(2)解:因为a∈M,所以 ![]() ,所以
,所以 ![]() .
.
因为|a﹣1|+|a+1|=a﹣1+a+1=2a≥3,
所以 ![]() ,
,
因为 ![]() =
= ![]() =
= ![]() ,
,
又由 ![]() ,知a﹣1>0,4a﹣3>0,
,知a﹣1>0,4a﹣3>0,
所以 ![]() ,
,
所以 ![]() ,
,
所以|a﹣1|+|a+1|> ![]()
【解析】(1)求出函数的分段函数的形式,求出f(x)的最小值,从而求出函数的值域即可;(2)根据绝对值的性质,求出a的范围,根据作差法比较即可.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.

【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.
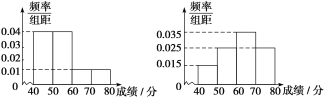
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)若称成绩在68分以上的学生知识渊博,试以上述数据估计该高一、高二两个年级学生的知识渊博率;
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.
分类 | 成绩低于60分人数 | 成绩不低于60分人数 | 总计 |
高一年级 | |||
高二年级 | |||
总计 |
附:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
K2=![]() .
.