题目内容
【题目】已知函数f(x)=kx3+3(k﹣1)x2﹣k2+1在x=0,x=4处取得极值.
(1)求常数k的值;
(2)求函数f(x)的单调区间与极值;
(3)设g(x)=f(x)+c,且x∈[﹣1,2],g(x)≥2c+1恒成立,求c的取值范围.
【答案】
(1)解:f'(x)=3kx2+6(k﹣1)x,由于在x=0,x=4处取得极值,
∴f'(0)=0,f'(4)=0,
可求得 ![]()
(2)解:由(1)可知 ![]() ,f'(x)=x2﹣4x=x(x﹣4),f'(x),f(x)随x的变化情况如下表:
,f'(x)=x2﹣4x=x(x﹣4),f'(x),f(x)随x的变化情况如下表:
x | (﹣∞,0) | 0 | (0,4) | 4 | (4,+∞) |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | 极大值 | 极小值 |
∴当x<0或x>4,f(x)为增函数,0≤x≤4,f(x)为减函数;
∴极大值为 ![]() ,极小值为
,极小值为 ![]()
(3)解:要使命题成立,需使g(x)的最小值不小于2c+1
由(2)得: ![]()
∴ ![]() ,
,
∴ ![]()
【解析】(1)因为函数两个极值点已知,令f′(x)=3kx2+6(k﹣1)x=0,把0和4代入求出k即可.(2)利用函数的导数确定函数的单调区间,f′(x)=3kx2+6(k﹣1)x=x2﹣4x=x(x﹣4)大于零和小于零分别求出递增和递减区间即可,把函数导数为0的x值代到f(x)中,通过表格,判断极大、极小值即可.(3)要使命题成立,需使g(x)的最小值不小于2c+1,由(2)得:g(﹣1)和g(2)其中较小的即为g(x)的最小值,列出不等关系即可求得c的取值范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.
在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.
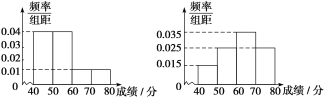
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)若称成绩在68分以上的学生知识渊博,试以上述数据估计该高一、高二两个年级学生的知识渊博率;
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.
分类 | 成绩低于60分人数 | 成绩不低于60分人数 | 总计 |
高一年级 | |||
高二年级 | |||
总计 |
附:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
K2=![]() .
.