Question

【题目】已知曲线C1:y=x2与曲线C2:y=-(x-2)2,直线l与C1和C2都相切,求直线l的方程.

Answer 1

【答案】或

【解析】

先设出直线与两曲线的切点坐标P(x1,)和Q(x2,-(x2-2)2)，根据导数的几何意义分别求出切线的方程，再根据两切线重合得到关于和的方程组，求得和后可得切线方程．

设l与C1相切于点P(x1,),与C2相切于点Q(x2,-(x2-2)2).

对于曲线C1，有y'=2x，

所以与C1相切于点P的切线方程为y-=2x1(x-x1)，

即y=2x1x．①

对于曲线C2，有y'=-2(x-2),

所以与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),

即y=-2(x2-2)x+．②

由题意得两切线重合，

所以由①②得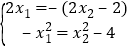，解得或．

所以直线l的方程为或．