题目内容
【题目】已知a,b,c分别为△ABC内角A,B,C的对边, ![]() .
.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC边AC上的高h=b,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)由 ![]() . 根据正弦定理,可得:
. 根据正弦定理,可得: ![]() ,
,
即a﹣bcosC=csinB,
得:sinA﹣sinBcosC=sinCsinB.
B+C+A=π
∴sinA=sin(B+C)
∴sinBcosC+sinCcosB﹣sinBcosC=sinCsinB.
可得:sinCcosB=sinCsinB.
∵0<C<π,sinC≠0.
∴cosB=sinB
∵0<B<π.
∴B= ![]() .
.
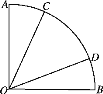
(Ⅱ)由题意,过B点作AC的高h=DB=b.设AD=m,DC=n,n+m=b.
则tanA= ![]() ,tanC=
,tanC= ![]() ,
,
可得 ![]() =sinB(
=sinB( ![]() )=sinB=
)=sinB= ![]() .
.
【解析】(Ⅰ)运用正弦定理结合三角形的内角和定理.即可得到A.(Ⅱ)根据△ABC边AC上的高h=b,求出tanA和tanC,带入化简可得答案.
【考点精析】关于本题考查的正弦定理的定义,需要了解正弦定理:![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目