题目内容
已知圆C的圆心在直线l1:2x-y+1=0上,与直线3x-4y+9=0相切,且截直线l3:4x-3y+3=0所得的弦长为2,求圆C的方程.
圆的方程为x2+(y-1)2=1或(x-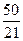 )2+(y-
)2+(y-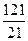 )2=(
)2=(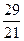 )2.
)2.
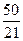 )2+(y-
)2+(y-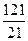 )2=(
)2=(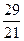 )2.
)2.设圆C的方程为(x-a)2+(y-b)2=r2,
则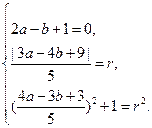
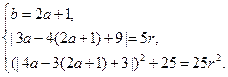
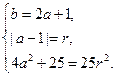
4a2+25=25(a-1)2.a=0或a=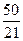 .
.
∴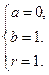 或
或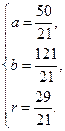
∴所求圆的方程为x2+(y-1)2=1或(x-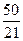 )2+(y-
)2+(y-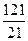 )2=(
)2=(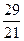 )2.
)2.
则
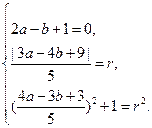
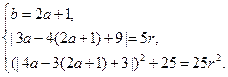
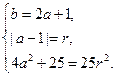
4a2+25=25(a-1)2.a=0或a=
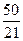 .
.∴
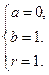 或
或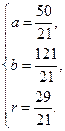
∴所求圆的方程为x2+(y-1)2=1或(x-
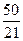 )2+(y-
)2+(y-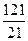 )2=(
)2=(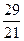 )2.
)2.
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
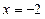 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线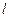 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为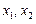 .①求证:
.①求证: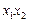 为定值;②试用
为定值;②试用 经过
经过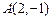 和直线
和直线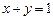 相切,且圆心在直线
相切,且圆心在直线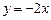 上.
上. 经过圆
经过圆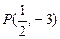 与圆
与圆 两点,当弦
两点,当弦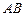 被点
被点 平分时,求直线
平分时,求直线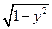 =x有两个不同交点,则实数m的取值范围为( )
=x有两个不同交点,则实数m的取值范围为( ) ,
,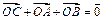 ,且
,且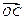 =
= a.
a.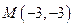 的直线
的直线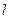 被圆
被圆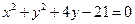 所截得的弦长为
所截得的弦长为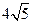 ,
,
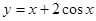 在
在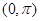 上的单调递减区间为 .
上的单调递减区间为 .