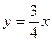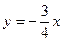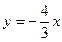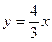题目内容
已知椭圆C中心在原点、焦点在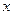 轴上,椭圆C上的点到焦点的最大值为
轴上,椭圆C上的点到焦点的最大值为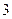 ,最小值为
,最小值为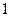 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线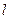 :
: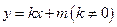 与椭圆交于不同的两点
与椭圆交于不同的两点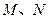 (
(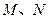 不是左、右顶点),且以
不是左、右顶点),且以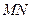 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点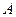 .求证:直线
.求证:直线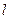 过定点,并求出定点的坐标
过定点,并求出定点的坐标
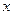 轴上,椭圆C上的点到焦点的最大值为
轴上,椭圆C上的点到焦点的最大值为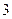 ,最小值为
,最小值为 .
.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线
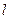 :
: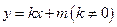 与椭圆交于不同的两点
与椭圆交于不同的两点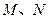 (
(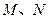 不是左、右顶点),且以
不是左、右顶点),且以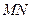 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点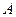 .求证:直线
.求证:直线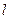 过定点,并求出定点的坐标
过定点,并求出定点的坐标(Ⅰ)
 (Ⅱ)
(Ⅱ) 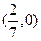
(Ⅰ)设椭圆的长半轴为
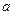 ,半焦距为
,半焦距为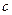 ,则
,则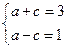 解得
解得 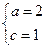
∴ 椭圆C的标准方程为
 . ………………… 4分
. ………………… 4分(Ⅱ)由方程组
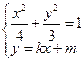 消去
消去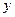 ,得
,得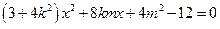
由题意:△
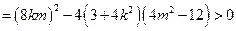
整理得:
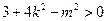 ① ……7分
① ……7分设
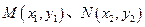 ,则
,则 ,
,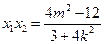 ………………… 8分
………………… 8分由已知,
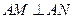 ,且椭圆的右顶点为
,且椭圆的右顶点为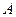
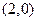
∴
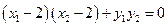 ………………… 10分
………………… 10分即
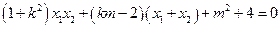
也即
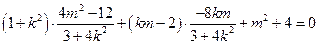
整理得:
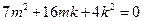
解得:
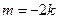 或
或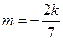 ,均满足① ……………………… 12分
,均满足① ……………………… 12分当
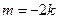 时,直线
时,直线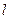 的方程为
的方程为 ,过定点
,过定点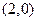 ,舍去
,舍去当
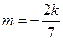 时,直线
时,直线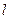 的方程为
的方程为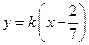 ,过定点
,过定点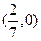 ,
,故,直线
 过定点,且定点的坐标为
过定点,且定点的坐标为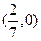 .……………………… 14分
.……………………… 14分
练习册系列答案
相关题目
 +
+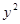 =1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )
=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )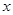 ;
; 经过
经过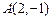 和直线
和直线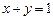 相切,且圆心在直线
相切,且圆心在直线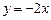 上.
上. 经过圆
经过圆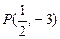 与圆
与圆 两点,当弦
两点,当弦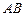 被点
被点 平分时,求直线
平分时,求直线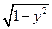 =x有两个不同交点,则实数m的取值范围为( )
=x有两个不同交点,则实数m的取值范围为( ) ,
,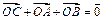 ,且
,且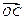 =
= a.
a.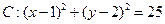
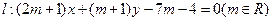
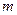 为何值时,直线和圆恒相交于两点;
为何值时,直线和圆恒相交于两点;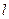 被圆
被圆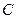 截得的弦长最小时的方程.
截得的弦长最小时的方程.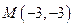 的直线
的直线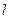 被圆
被圆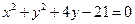 所截得的弦长为
所截得的弦长为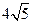 ,
,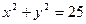 截直线
截直线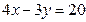 所得弦的垂直平分线方程是( ).
所得弦的垂直平分线方程是( ).