题目内容
17.已知正数数列{an}满足:数列{a2n-1}是首项为1的等比数列,数列{a2n}是首项为2的等差数列.设数列{an}的前n项和为Sn(n∈N*),已知S3=a4,a2+a3+a5=a6.(1)求数列{an}的通项公式;
(2)求数列{an}的前2m项和S2m.
分析 (1)设数列{a2n-1}是首项为1,公比为q的等比数列,数列{a2n}是首项为2,公差为d的等差数列,运用等比数列和等差数列的通项公式,列方程,解得q,d,即可得到通项公式;
(2)运用数列的求和方法:分组求和,由等比数列和等差数列的求和公式,化简即可得到.
解答 解:(1)设数列{a2n-1}是首项为1,公比为q的等比数列,
数列{a2n}是首项为2,公差为d的等差数列,
由S3=a4,a2+a3+a5=a6.
即有3+q=2+d,2+q+q2=2+2d,
解得q=2,d=3或q=-1,d=0(舍去),
则有an=$\left\{\begin{array}{l}{{2}^{k-1},n=2k-1}\\{3k-1,n=2k}\end{array}\right.$;
(2)S2m=(a1+a3+a5+…+a2m-1)+(a2+a4+a6+…+a2m)
=(1+2+4+…+2m-1)+[2+5+8+…+(3m-1)]
=$\frac{1-{2}^{m}}{1-2}$+$\frac{m(2+3m-1)}{2}$
=2m-1+$\frac{3}{2}$m2+$\frac{1}{2}$m.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查运算能力,注意运用分组求和,属于中档题.

练习册系列答案
相关题目
7.某产品的广告费用支出x与销售额y(单位:百万元)之间有如下的对应数据:
(1)求y与x之间的回归直线方程;(参考数据:22+42+52+62+82=145,2×30+4×40+5×60+6×50+8×70=1380)
(2)试预测广告费用支出为1千万元时,销售额是多少?
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费用支出为1千万元时,销售额是多少?
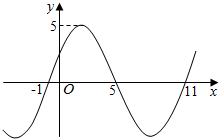 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.