题目内容
9.已知函数f(x)=|x-1|,设f1(x)=f(x),fn(x)=fn-1(f(x))(n>1,n∈N*),令函数F(x)=fn(x)-m,若m∈(0,1)时,函数F(x)有且只有8各不同的零点,这8个零点按从小到大的顺序分别记为x1、x2、x3、x4、x5、x6、x7、x8,则x1x2x5x6+x3x4x7x8的取值范围是(-6,16).分析 由题意作函数fn(x)的图象,再设x4=x,x∈(0,1);从而可得x3=-x,x2=x-2,x1=-x-2,x5=-x+2,x6=x+2,x7=-x+4,x8=x+4;从而化简即可.
解答 解:由题意,作fn(x)的图象如下,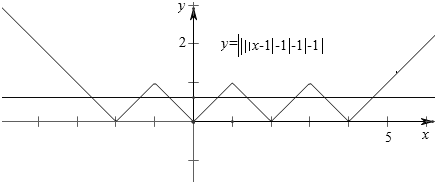
结合图象可得,
设x4=x,x∈(0,1);则x3=-x,x2=x-2,x1=-x-2,
x5=-x+2,x6=x+2,x7=-x+4,x8=x+4;
故x1x2x5x6+x3x4x7x8=(-x-2)(x-2)(-x+2)(x+2)+(-x)x(-x+4)(x+4)
=(4-x2)2-x2(16-x2)=2(x2)2-24x2+16=2(x2-6)2-56
∵x∈(0,1),
∴x2-6∈(-6,-5),
∴50<2(x2-6)2<72,
∴-6<2(x2-6)2-56<16,
故x1x2x5x6+x3x4x7x8的取值范围是(-6,16);
故答案为:(-6,16).
点评 本题考查了数形结合的思想应用及函数的零点与函数的图象的关系应用,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20.已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )
| A. | (1,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-∞,-2) |
14.设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$,且$|\begin{array}{l}{\overrightarrow{a}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{b}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{c}}\\{\;}\end{array}|$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |