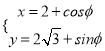题目内容
【题目】已知函数f（x）=（x﹣a）2lnx（a为常数）．
（1）若f（x）在（1，f（1））处的切线与直线2x+2y﹣3=0垂直．
（ⅰ）求实数a的值；
（ⅱ）若a非正，比较f（x）与x（x﹣1）的大小；
（2）如果0＜a＜1，判断f（x）在（a，1）上是否有极值，若有极值是极大值还是极小值？若无极值，请说明理由．
【答案】
（1）解：（ⅰ）f（x）定义域是（0，+∞），f′（x）=（x﹣a）（2lnx+ 
），
∵直线2x+2y﹣3=0的斜率为：k=﹣1，
∴f（x）在（1，f（1））处的切线的斜率﹣ 
=1，
即f′（1）=（1﹣a）（2ln1+ 
）=（1﹣a）2=1，
∴a=0或a=2；
（ⅱ）由（ⅰ）知，a=0，∴f（x）=x2lnx，
∵x2lnx﹣x（x﹣1）=x（xlnx﹣x+1），
∴令g（x）=xlnx﹣x+1，g′（x）=lnx，
当x＞1时，g′（x）＞0，当0＜x＜1时，g′（x）＜0，
∴g（x）在（0，1）单调递减，在（1，+∞）单调递增，
g（x）min=g（1）=0，∴g（x）≥0恒成立，
即f（x）≥x（x﹣1）；
（2）解：f′（x）=（x﹣a）（2lnx+ ），
令F（x）=2lnx+1﹣ 
，F′（x）= 
＞0，
∴F（x）在（a，1）上单调递增，又F（1）=1﹣a＞0，F（a）=2lna＜0，
所以在（a，1）上必存在x0，使F（x0）=0，
又x﹣a＞0，∴当x∈（a，x0），f′（x）＜0，x∈（x0，1），f′（x）＞0，
∴f（x）在（a，x0）单调递减，在（x0，1）单调递增，
∴x=x0是f（x）的极值点，且为极小值．
【解析】（1）（i）求出f（x）的导数，根据切线的斜率是f′（1）=﹣ =1，解出a的值即可；（ii）求出f（x）的表达式，作差，得到x2lnx﹣x（x﹣1）=x（xlnx﹣x+1），令g（x）=xlnx﹣x+1，根据函数的单调性求出g（x）的最小值g（1）=0，得到g（x）≥0恒成立，从而求出f（x）与x（x﹣1）的大小即可；（2）求出f′（x）=（x﹣a）（2lnx+ ），令F（x）=2lnx+1﹣ ，求出F（x）的导数，根据函数的单调性求出函数的极值即可．
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案，需要熟知求函数
的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧
,右侧
,那么
是极小值．
