题目内容
3.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=t+1}\\{y=2t}\end{array}\right.$( 为参数),曲线C的参数方程为$\left\{\begin{array}{l}x=2{t}^{2}\\ y=2t\end{array}\right.$(t为参数).试求直线l和曲线C的普通方程,并求出它们的公共点的坐标.分析 运用代入法,可将直线l和曲线C的参数方程化为普通方程,联立直线方程和抛物线方程,解方程可得它们的交点坐标.
解答 解:直线l的参数方程为$\left\{\begin{array}{l}{x=t+1}\\{y=2t}\end{array}\right.$( 为参数),
由x=t+1可得t=x-1,代入y=2t,
可得直线l的普通方程:2x-y-2=0.
曲线C的参数方程为$\left\{\begin{array}{l}{x=2{t}^{2}}\\{y=2t}\end{array}\right.$(t为参数),化为y2=2x,
联立$\left\{\begin{array}{l}{y=2(x-1)}\\{{y}^{2}=2x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-1}\end{array}\right.$,
于是交点为(2,2),$(\frac{1}{2},-1)$.
点评 本题主要考查了参数方程与普通方程的互化、直线与抛物线的位置关系等基础知识,考查了转化能力,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
16.已知i是虚数单位,若复数z满足z=$\frac{25}{3-4i}$,则z的共轭复数$\overline{z}$为( )
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
8.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是( )
| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
 .
. 是不是该数列中的项,为什么?
是不是该数列中的项,为什么? 内有、无数列中的项?若有,有几项?若没有,说明理由.
内有、无数列中的项?若有,有几项?若没有,说明理由.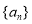 中,
中,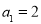 ,
,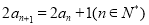 ,则
,则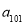 的值为( )
的值为( )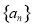 的公差为
的公差为 ,前
,前 项和为
项和为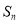 ,若
,若 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( ) B.
B.
 D.
D.