题目内容
14.已知椭圆x2+2y2=1,过原点的两条直线l1和l2分别于椭圆交于A、B和C、D,记得到的平行四边形ACBD的面积为S.(1)设A(x1,y1),C(x2,y2),用A、C的坐标表示点C到直线l1的距离,并证明S=2|x1y2-x2y1|;
(2)设l1与l2的斜率之积为-$\frac{1}{2}$,求面积S的值.
分析 (1)依题意,直线l1的方程为y=$\frac{{y}_{1}}{{x}_{1}}$x,利用点到直线间的距离公式可求得点C到直线l1的距离d=$\frac{|{y}_{1}{x}_{2}-{x}_{1}{y}_{2}|}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}$,再利用|AB|=2|AO|=2$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$,可证得S=|AB|d=2|x1y2-x2y1|;当l1与l2时的斜率之一不存在时,同理可知结论成立;
(2)方法一:设直线l1的斜率为k,则直线l2的斜率为-$\frac{1}{2k}$,可得直线l1与l2的方程,联立方程组$\left\{\begin{array}{l}y=kx\\{x}^{2}+2{y}^{2}=1\end{array}\right.$,可求得x1、x2、y1、y2,继而可求得答案.
方法二:设直线l1、l2的斜率分别为$\frac{{y}_{1}}{{x}_{1}}$、$\frac{{y}_{2}}{{x}_{2}}$,则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,利用A(x1,y1)、C(x2,y2)在椭圆x2+2y2=1上,可求得面积S的值.
解答 解:(1)依题意,直线l1的方程为y=$\frac{{y}_{1}}{{x}_{1}}$x,由点到直线间的距离公式得:点C到直线l1的距离d=$\frac{|\frac{{y}_{1}{x}_{2}}{{x}_{1}}-{y}_{2}|}{\sqrt{1+{(\frac{{y}_{1}}{{x}_{1}})}^{2}}}$=$\frac{|{y}_{1}{x}_{2}-{x}_{1}{y}_{2}|}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}$,
因为|AB|=2|AO|=2$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$,所以S=|AB|d=2|x1y2-x2y1|;
当l1与l2时的斜率之一不存在时,同理可知结论成立;
(2)方法一:设直线l1的斜率为k,则直线l2的斜率为-$\frac{1}{2k}$,
设直线l1的方程为y=kx,联立方程组$\left\{\begin{array}{l}y=kx\\{x}^{2}+2{y}^{2}=1\end{array}\right.$,消去y解得x=±$\frac{1}{\sqrt{1+2{k}^{2}}}$,
根据对称性,设x1=$\frac{1}{\sqrt{1+2{k}^{2}}}$,则y1=$\frac{k}{\sqrt{1+2{k}^{2}}}$,
同理可得x2=$\frac{\sqrt{2}k}{\sqrt{1+2{k}^{2}}}$,y2=$\frac{-\frac{\sqrt{2}}{2}}{\sqrt{1+2{k}^{2}}}$,所以S=2|x1y2-x2y1|=$\sqrt{2}$.
方法二:设直线l1、l2的斜率分别为$\frac{{y}_{1}}{{x}_{1}}$、$\frac{{y}_{2}}{{x}_{2}}$,则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,
所以x1x2=-2y1y2,
∴${{x}_{1}}^{2}{{x}_{2}}^{2}$=4${{y}_{1}}^{2}{{y}_{2}}^{2}$=-2x1x2y1y2,
∵A(x1,y1)、C(x2,y2)在椭圆x2+2y2=1上,
∴(${{x}_{1}}^{2}{{+2y}_{1}}^{2}$)(${{x}_{2}}^{2}{{+2y}_{2}}^{2}$)=${{x}_{1}}^{2}{{x}_{2}}^{2}$+4${{y}_{1}}^{2}{{y}_{2}}^{2}$+2(${{x}_{1}}^{2}{{y}_{2}}^{2}$+${{x}_{2}}^{2}{{y}_{1}}^{2}$)=1,
即-4x1x2y1y2+2(${{x}_{1}}^{2}{{y}_{2}}^{2}$+${{x}_{2}}^{2}{{y}_{1}}^{2}$)=1,
所以(x1y2-x2y1)2=$\frac{1}{2}$,即|x1y2-x2y1|=$\frac{\sqrt{2}}{2}$,
所以S=2|x1y2-x2y1|=$\sqrt{2}$.
点评 本题考查直线与圆锥曲线的综合应用,考查方程思想、等价转化思想与综合运算能力,属于难题.

 口算题天天练系列答案
口算题天天练系列答案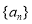 满足
满足
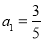 ,则数列的第2015项为_________.
,则数列的第2015项为_________. ,如果
,如果 ,那么
,那么 等于( )
等于( ) 被圆
被圆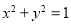 截得的弦长为
截得的弦长为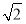 ,则
,则 ___________.
___________.