题目内容
12.判断并证明函数f(x)=loga$\frac{1-x}{1+x}$(a>0,a≠1)的单调性.分析 先求出函数f(x)的定义域为(-1,1),求f′(x),讨论0<a<1,和a>1两种情况,并判断每种情况下f′(x)的符号,从而判断出f(x)的单调性.
解答 解:函数f(x)的定义域为(-1,1);
f′(x)=$\frac{2}{({x}^{2}-1)lna}$;
∵x∈(-1,1);
∴x2-1<0;
∴①若0<a<1,lna<0,则f′(x)>0;
∴f(x)在(-1,1)上单调递增;
②若a>1,lna>0,则f′(x)<0;
∴f(x)在(-1,1)上单调递减.
点评 考查对数中真数的取值情况,解分式不等式,复合函数的求导,以及对数函数的单调性,清楚需讨论0<a<1和a>1两种情况,函数导数符号和函数单调性的关系,并注意正确求导.

练习册系列答案
相关题目
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1,F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的离心率为( )
| A. | $\sqrt{2\sqrt{5}+3}$ | B. | $\sqrt{2\sqrt{5}-3}$ | C. | $\sqrt{5+2\sqrt{3}}$ | D. | $\sqrt{5-2\sqrt{3}}$ |
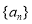 满足
满足
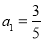 ,则数列的第2015项为_________.
,则数列的第2015项为_________. 为自然对数的底数.
为自然对数的底数. 在区间
在区间 上的最值;
上的最值; 时,设函数
时,设函数 (其中
(其中 为常数)的3个极值点为
为常数)的3个极值点为 ,且
,且 ,将
,将 这5个数按照从小到大的顺序排列,并证明你的结论.
这5个数按照从小到大的顺序排列,并证明你的结论.