题目内容
8.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是( )| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
分析 作差法逐个选项比较大小可得.
解答 解:∵x<y<z且a<b<c,
∴ax+by+cz-(az+by+cx)
=a(x-z)+c(z-x)
=(x-z)(a-c)>0,
∴ax+by+cz>az+by+cx;
同理ay+bz+cx-(ay+bx+cz)
=b(z-x)+c(x-z)
=(z-x)(b-c)<0,
∴ay+bz+cx<ay+bx+cz;
同理az+by+cx-(ay+bz+cx)
=a(z-y)+b(y-z)
=(z-y)(a-b)<0,
∴az+by+cx<ay+bz+cx,
∴最低费用为az+by+cx
故选:B
点评 本题考查函数的最值,涉及作差法比较不等式的大小,属中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1.集合P={x|$\frac{x-1}{x+3}$>0},Q={x|y=$\sqrt{4-{x}^{2}}$},则P∩Q=( )
| A. | (1,2] | B. | [1,2] | C. | (-∞,-3)∪(1,+∞) | D. | [1,2) |
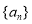 中,
中,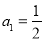 ,
,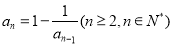 .
.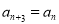 ;
;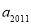 .
.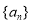 满足
满足
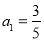 ,则数列的第2015项为_________.
,则数列的第2015项为_________.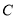 :
: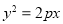 (
( )与椭圆
)与椭圆 :
: 相交所得的弦长为
相交所得的弦长为 .
. 的标准方程;
的标准方程; ,
, 是
是 上异于原点
上异于原点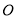 的两个不同点,直线
的两个不同点,直线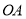 和
和 的倾斜角分别为
的倾斜角分别为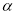 和
和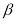 ,当
,当 ,
,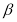 变化且
变化且 为定值
为定值 (
( )时,证明:直线
)时,证明:直线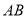 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.