题目内容
17.(1)已知2${\;}^{{x}^{2}+x}$<($\frac{1}{4}$)x-2,求函数y=2-x的值域.(2)已知$\overrightarrow{a}$=($\sqrt{3}$,1),$\overrightarrow{b}$=($\sqrt{3}$,0),求<$\overrightarrow{a},\overrightarrow{b}$>
分析 (1)运用指数函数的单调性,解不等式可得-4<x<1,再由指数函数的单调性,即可得到所求值域;
(2)运用平面向量的数量积的坐标表示和斜率的模的公式,计算即可得到所求夹角.
解答 解:(1)不等式2${\;}^{{x}^{2}+x}$<($\frac{1}{4}$)x-2,
即为${2}^{{x}^{2}+x}$<24-2x,
即有x2+x<4-2x,
解得-4<x<1,
即有-1<-x<4,
则函数y=2-x的值域为($\frac{1}{2}$,16);
(2)由$\overrightarrow{a}$=($\sqrt{3}$,1),$\overrightarrow{b}$=($\sqrt{3}$,0),
则$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}×\sqrt{3}$+1×0=3,
|$\overrightarrow{a}$|=$\sqrt{3+1}$=2,|$\overrightarrow{b}$|=$\sqrt{3}$,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,
则<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{6}$.
点评 本题考查指数函数的单调性的运用:解不等式和求值域,同时考查平面向量的数量积的坐标表示和夹角的求法,属于中档题.

| A. | $\sqrt{2\sqrt{5}+3}$ | B. | $\sqrt{2\sqrt{5}-3}$ | C. | $\sqrt{5+2\sqrt{3}}$ | D. | $\sqrt{5-2\sqrt{3}}$ |
 被圆
被圆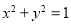 截得的弦长为
截得的弦长为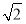 ,则
,则 ___________.
___________.