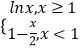题目内容
【题目】记Sn为等比数列![]() 的前n项和,已知S2=2,S3=-6.
的前n项和,已知S2=2,S3=-6.
(1)求![]() 的通项公式;
的通项公式;
(2)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列。
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由等比数列通项公式解得![]() ,
, ![]() 即可求解;(2)利用等差中项证明Sn+1,Sn,Sn+2成等差数列.
即可求解;(2)利用等差中项证明Sn+1,Sn,Sn+2成等差数列.
试题解析:(1)设![]() 的公比为
的公比为![]() .由题设可得
.由题设可得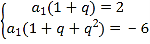 ,解得
,解得![]() ,
, ![]() .
.
故![]() 的通项公式为
的通项公式为![]() .
.
(2)由(1)可得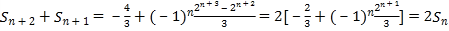 .
.
由于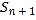 ,
,
故![]() ,
, ![]() ,
, ![]() 成等差数列.
成等差数列.
点睛:等差、等比数列的性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形.在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目