题目内容
【题目】中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美，给出定义：能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”，给出下列命题：
①对于任意一个圆O，其“优美函数“有无数个”；
②函数 
可以是某个圆的“优美函数”；
③正弦函数y=sinx可以同时是无数个圆的“优美函数”；
④函数y=f（x）是“优美函数”的充要条件为函数y=f（x）的图象是中心对称图形．
其中正确的命题是（ ）
A.①③
B.①③④
C.②③
D.①④
【答案】A
【解析】解：过圆心的直线都可以将圆的周长和面积同时平分，
故对于任意一个圆O，其“优美函数”有无数个，故①正确；
函数 
的大致图象如图1，故其不可能为圆的“优美函数”；∴②不正确；
将圆的圆心放在正弦函数y=sinx的对称中心上，
则正弦函数y=sinx是该圆的“优美函数”；
故有无数个圆成立，故③正确；
函数y=f（x）的图象是中心对称图形，则y=f（x）是“优美函数”，
但函数y=f（x）是“优美函数”时，图象不一定是中心对称图形，如图2，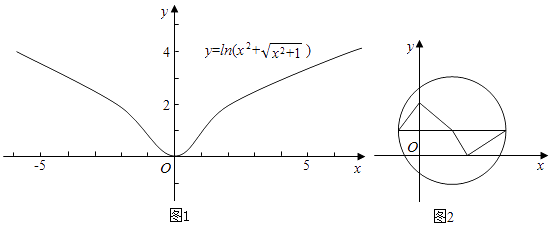
故选：A．
过圆心的直线都可以将圆的周长和面积同时平分，故①正确；
作函数 的大致图象，从而判断②的正误；
将圆的圆心放在正弦函数y=sinx的对称中心上，则正弦函数y=sinx是该圆的“优美函数”；即可判断③的正误；
函数y=f（x）的图象是中心对称图形，则y=f（x）是“优美函数”，但函数y=f（x）是“优美函数”时，图象不一定是中心对称图形，作图举反例即可．
名校课堂系列答案
【题目】为了对2016年某校中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学分数（已折算为百分制）从小到大排是60、65、70、75、80、85、90、95，物理分数从小到大排是72、77、80、84、88、90、93、95． 参考公式：相关系数 
，
回归直线方程是： 
，其中 
，
参考数据： 
， 
， 
， 
．
（1）若规定85分以上为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；
（2）若这8位同学的数学、物理、化学分数事实上对应如下表：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度；
②求y与x、z与x的线性回归方程（系数精确到0.01），当某同学的数学成绩为50分时，估计其物理、化学两科的得分．
