题目内容
【题目】已知函数f(x)= 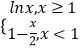 ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,4﹣2ln2]
D.(﹣∞, ![]() )
)
【答案】D
【解析】解:当x≥1时,f(x)=lnx≥0, ∴f(x)+1≥1,
∴f[f(x)+1]=ln(f(x)+1),
当x<1,f(x)=1﹣ ![]() >
> ![]() ,f(x)+1>
,f(x)+1> ![]() ,
,
f[f(x)+1]=ln(f(x)+1),
综上可知:F[f(x)+1]=ln(f(x)+1)+m=0,
则f(x)+1=e﹣m , f(x)=e﹣m﹣1,有两个根x1 , x2 , (不妨设x1<x2),
当x≥1是,lnx2=e﹣m﹣1,当x<1时,1﹣ ![]() =e﹣m﹣1,
=e﹣m﹣1,
令t=e﹣m﹣1> ![]() ,则lnx2=t,x2=et , 1﹣
,则lnx2=t,x2=et , 1﹣ ![]() =t,x1=2﹣2t,
=t,x1=2﹣2t,
∴x1x2=et(2﹣2t),t> ![]() ,
,
设g(t)=et(2﹣2t),t> ![]() ,
,
求导g′(t)=﹣2tet ,
t∈( ![]() ,+∞),g′(t)<0,函数g(t)单调递减,
,+∞),g′(t)<0,函数g(t)单调递减,
∴g(t)<g( ![]() )=
)= ![]() ,
,
∴g(x)的值域为(﹣∞, ![]() ),
),
∴x1x2取值范围为(﹣∞, ![]() ),
),
故选:D.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目