题目内容
10.已知数列{an}中,an=(-1)nn2,求Sn.分析 直接分n为奇数和偶数写出数列的和,因式分解后化为等差数列,由等差数列的前n项和得答案.
解答 解:由an=(-1)nn2,
当n为奇数时,
${S}_{n}=-{1}^{2}+{2}^{2}-{3}^{2}+{4}^{2}-…-(n-2)^{2}+(n-1)^{2}$-n2
=1×3+1×7+1×11+…+1×(2n-3)-n2
=3+7+11+…+(2n-3)-n2
=$\frac{(3+2n-3)×\frac{n-1}{2}}{2}-{n}^{2}$=$-\frac{n(n+1)}{2}$;
当n为偶数时,
${S}_{n}=-{1}^{2}+{2}^{2}-{3}^{2}+{4}^{2}-…-(n-1)^{2}+{n}^{2}$
=3+7+11+…+(2n-1)
=$\frac{(3+2n-1)×\frac{n}{2}}{2}=\frac{n(n+1)}{2}$.
∴${S}_{n}=\left\{\begin{array}{l}{-\frac{n(n+1)}{2},n为奇数}\\{\frac{n(n+1)}{2},n为偶数}\end{array}\right.$.
点评 本题考查了等差关系的确定,考查了等差数列的前n项和,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
1.下列函数中,在区间(0,+∞)上为增函数的是( )
| A. | y=x-1 | B. | y=ln(x+1) | C. | y=($\frac{1}{2}$)x | D. | y=x+$\frac{1}{x}$ |
15.命题“任意x≥0,都有2x≥1”的否定,叙述正确的是( )
| A. | 存在x<0,使得2x≥1 | B. | 任意x<0,都有2x<1 | ||
| C. | 存在x<0,使得AF∥平面BCE | D. | 存在x≥0,使得2x<1 |
19.已知两点M(-1,0),N(1,0),若直线y=k(x-2)上存在点P,使得PM⊥PN,则实数k的取值范围是( )
| A. | $[-\frac{1}{3},0)∪(0,\frac{1}{3}]$ | B. | [-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-5,5] |
20.i是虚数单位,复数$\frac{-1+2i}{3+4i}$=( )
| A. | $\frac{1}{5}+\frac{2}{5}i$ | B. | $-\frac{1}{5}+\frac{2}{5}i$ | C. | 1-2i | D. | -1-2i |
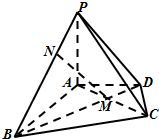 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.