题目内容
18.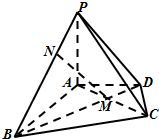 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.(I)求证:MN∥平面PDC;
(Ⅱ)求直线PB与平面PAC所成角的正弦值.
分析 (Ⅰ)通过证明MN∥PD,利用直线与平面平行的判定定理证明MN∥平面PDC.
(Ⅱ)说明∠BPM就是直线PB与平面PAC所成角,然后求解直线PB与平面PAC所成角的正弦值.
解答  解:(Ⅰ)在正三角形ABC中,$BM=2\sqrt{3}$,
解:(Ⅰ)在正三角形ABC中,$BM=2\sqrt{3}$,
在△ACD中,因为M为AC中点,DM⊥AC,所以AD=CD,∠CDA=120°,
所以$DM=\frac{{2\sqrt{3}}}{3}$,所以BM:MD=3:1…(4分)
在等腰直角三角形PAB中,$PA=AB=4,PB=4\sqrt{2}$,
所以BN:NP=3:1,BN:NP=BM:MD,所以MN∥PD,
又MN?平面PDC,PD?平面PDC,所以MN∥平面PDC;…(7分)
(Ⅱ)在正三角形ABC中,BM⊥AC,
又因为PA⊥平面ABCD,BM?平面ABCD,所以PA⊥BM,
而PA∩AC=A,因此BM⊥平面PAC,
连结PM,因此∠BPM就是直线PB与平面PAC所成角;…(10分)
在直角三角形PBM中,$BM=2\sqrt{3},PB=4\sqrt{2}$,
因此,$sin∠BPM=\frac{BM}{PB}=\frac{{2\sqrt{3}}}{{4\sqrt{2}}}=\frac{{\sqrt{6}}}{4}$…(15分)
点评 本题考查直线与平面所成角,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
8.下列函数中,既是奇函数又存在极值的函数是( )
| A. | y=x3 | B. | $y=x+\frac{1}{x}$ | C. | y=x•e-x | D. | y=ln(-x) |
3.已知动点P(x,y)满足约束条件$\left\{\begin{array}{l}{y≥2|x|-1}\\{y≤x+1}\end{array}\right.$,则z=|2x-3y-6|的最小值是3.
7.设i为虚数单位,若$\frac{a+2i}{i}$=b-i(a,b∈R),则a+b=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的一条渐近线与$y=\sqrt{3}x-1$平行,且它的一个焦点在抛物线x2=24y的准线上,则双曲线的方程为( )
| A. | $\frac{y^2}{36}-\frac{x^2}{108}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{108}-\frac{x^2}{36}=1$ | D. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ |
 如图,已知F为抛物线y2=4x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F.
如图,已知F为抛物线y2=4x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F.