题目内容
14.复数$\frac{a+i}{2-i}$在复平面内所对应的点在虚轴上,则实数a=$\frac{1}{2}$.分析 利用复数代数形式的乘除运算化简,然后由实部等于0且虚部吧等于0求得a的值.
解答 解:∵$\frac{a+i}{2-i}$=$\frac{(a+i)(2+i)}{(2-i)(2+i)}=\frac{2a-1+(a+2)i}{5}$,
又复数$\frac{a+i}{2-i}$在复平面内所对应的点在虚轴上,则
$\left\{\begin{array}{l}{2a-1=0}\\{a+2≠0}\end{array}\right.$,即a=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.

练习册系列答案
相关题目
4. 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
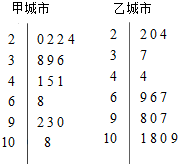
甲、乙两城市2015年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
(Ⅰ)根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数,并分析两城市空气质量哪个较好?
(Ⅱ)王先生到乙地出差5天,已知该5天是空气质量最好的五天,王先生要在这5天中选择两天出去游玩,求这两天恰好有一天空气质量类别为优的概率.
 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数,并分析两城市空气质量哪个较好?
(Ⅱ)王先生到乙地出差5天,已知该5天是空气质量最好的五天,王先生要在这5天中选择两天出去游玩,求这两天恰好有一天空气质量类别为优的概率.
5.已知集合A={x|$\frac{x}{x-1}$≥0,x∈R},B={y|y=2x+1,x∈R},则A∩B=( )
| A. | (1,+∞) | B. | (-∞,0) | C. | (0,1] | D. | [0,1] |
19.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | y=x3 | B. | y=$\sqrt{x}$ | C. | y=cosx | D. | y=2|x| |
3.数列{an}满足a1=1,a2=$\frac{1}{2}$,并且an(an-1+an+1)=2an+1an-1(n≥2),则该数列的第2015项为( )
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{{2}^{2014}}$ | C. | $\frac{1}{2015}$ | D. | $\frac{1}{{2}^{2015}}$ |
4.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△ABO的面积为$\sqrt{3}$,则p的值为( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |