题目内容
19.已知在△ABC中,点A(-1,2),点B(3,-4),点C(2,7),求△ABC的面积.分析 由两点间距离公式可得|AB|,利用点斜式可得直线AB方程,利用点到直线的距离公式,可得点C到直线AB的距离h,根据三角形面积公式可得答案.
解答 解:设AB边上的高为h,则S△ABC=$\frac{1}{2}$|AB|•h.
|AB|=$\sqrt{(-1-3)^{2}+(2+4)^{2}}$=2$\sqrt{13}$,
AB边上的高h就是点C到AB的距离.
AB边所在的直线方程为3x+2y-1=0.
点C(2,7)到3x+2y-1=0的距离h=$\frac{|3×2+2×7-1|}{\sqrt{{3}^{2}+{2}^{2}}}$=$\frac{19}{\sqrt{13}}$,
因此,S△ABC=$\frac{1}{2}$×2$\sqrt{13}$×$\frac{19}{\sqrt{13}}$=19.
点评 本题考查三角形面积公式、两点间距离公式、点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
7.若执行如图所示的程序框图,则输出的i的值为( )
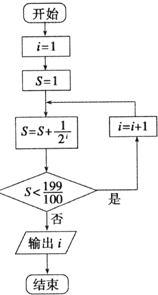

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
4.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△ABO的面积为$\sqrt{3}$,则p的值为( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
11.复数$\frac{3+2i}{1-i}$=( )
| A. | $\frac{1}{2}+\frac{5}{2}i$ | B. | $\frac{1}{2}-\frac{5}{2}i$ | C. | $-\frac{1}{2}+\frac{5}{2}i$ | D. | $-\frac{1}{2}-\frac{5}{2}i$ |
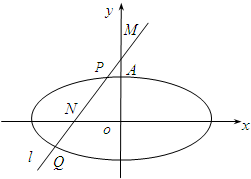 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.