题目内容
19.函数$f(x)=\sqrt{|x+1|+|x+2|-a}$.(1)a=5,函数f(x)的定义域A;
(2)设B={x|-1<x<2},当实数a,b∈(B∩CRA)时,证明:$\frac{|a+b|}{2}<|1+\frac{ab}{4}|$.
分析 (1)根据绝对值的几何意义即可求出,
(2)先两边平方,再利用做差法进行比较即可.
解答 解:(1)由|x+1|+|x+2|-5≥0,|x+1|+|x+2|≥5得到得A={x|x≤-4或x≥1},
(2)由A={x|x≤-4或x≥1},
∴CRA=(-4,1),
∵B={x|-1<x<2},
∴B∩CRA=(-1,1),
又$\frac{|a+b|}{2}<|1+\frac{ab}{4}|?2|a+b|<|4+ab|$
而4(a+b)2-(4+ab)2=4(a2+2ab+b2)-(16+8ab+a2b2)=4a2+4b2-a2b2-16=a2(4-b2)+4(b2-4)=(b2-4)(4-a2),
∵a,b∈(-1,1),
∴(b2-4)(4-a2)<0
∴4(a+b)2<(4+ab)2,
∴2|a+b|<|4+ab|
∴$\frac{|a+b|}{2}<|1+\frac{ab}{4}|$,
点评 本题考查绝对值的几何意义,集合的基本运算,以及不等式的证明,属于中档题.

练习册系列答案
相关题目
12.已知复数z满足:zi=1+i(i是虚数单位),则z的虚部为( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
7.若函数f(x)=(1-x2)(x2+ax+b)的图象关于直线x=2对称,则f(x)的最大值是( )
| A. | 9 | B. | 14 | C. | 15 | D. | 16 |
4.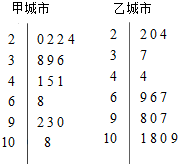 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
甲、乙两城市2015年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
(Ⅰ)根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数,并分析两城市空气质量哪个较好?
(Ⅱ)王先生到乙地出差5天,已知该5天是空气质量最好的五天,王先生要在这5天中选择两天出去游玩,求这两天恰好有一天空气质量类别为优的概率.
 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数,并分析两城市空气质量哪个较好?
(Ⅱ)王先生到乙地出差5天,已知该5天是空气质量最好的五天,王先生要在这5天中选择两天出去游玩,求这两天恰好有一天空气质量类别为优的概率.