题目内容
【题目】若函数f（x）=2|x﹣4|﹣logax+2无零点，则实数a的取值范围为;
若函数f（x）=|2x﹣2|﹣b有两个零点，则实数b的取值范围是 ．
【答案】（ 
，+∞）；（0，2）
【解析】解：⑴函数f（x）=2|x﹣4|﹣logax+2无零点，即方程2|x﹣4|﹣logax+2=0无实根，
也就是y=2|x﹣4|+2与y=logax的图象无交点，
作出两函数图象如图：
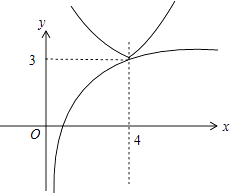
要使y=2|x﹣4|+2与y=logax的图象无交点，则loga4＜3，即a＞ ，
所以答案是：（ ，+∞）；
⑵函数f（x）=|2x﹣2|﹣b有两个零点，即方程函数|2x﹣2|﹣b=0有两个根，
也就是y=|2x﹣2|与y=b有两个交点，
如图：
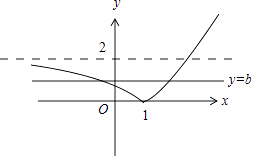
由图可知，要使y=|2x﹣2|与y=b有两个交点，则0＜b＜2．
所以答案是：（0，2）．
练习册系列答案
相关题目
