题目内容
【题目】设F1、F2分别为椭圆Γ： 
=1（a＞b＞0）的左、右两个焦点，若椭圆上一点M（1， 
）到两个焦点的距离之和等于4．又已知点A是椭圆的右顶点，直线l交椭圆Γ于E、F两点（E、F与A点不重合），且满足AE⊥AF． （Ⅰ） 求椭圆的标准方程；
（Ⅱ） O为坐标原点，若点P满足2 
，求直线AP的斜率的取值范围．
【答案】解：（Ⅰ）依题意，可得2a=4，即a=2，又点 
在椭圆上， 将点M（1， 
）代入椭圆方程可知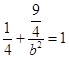 
，
解得：b2=3，
∴椭圆Γ的标准方程为 
；
（Ⅱ） 由（Ⅰ）知A（2，0），设直线AE的方程为y=k（x﹣2），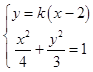
，整理得：（3+4k2）x2﹣16k2x+16k2﹣12=0，
由韦达定理可知：2+xE= 
，可得xE= 
，
yE=k（xE﹣2）= 
，
由于AE⊥AF，只要将上式的k换为﹣ 
，
可得xF= ，yF= 
，
由2 
，可得P为EF的中点，
即有P（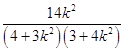 
， 
），
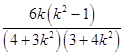则直线AP的斜率为t= 
= 
，
当k=0时，t=0；
当k≠0时，t=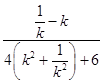 
，
再令s= 
，可得t= 
，
当s=0时，t=0；当s＞0时，t=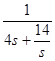 
≤ 
= 
，
当且仅当4s= 
时，取得最大值；
当s＜0时，t= ≥﹣ ，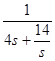
综上可得：直线AP的斜率的取值范围是[﹣ ， ]
【解析】（Ⅰ）由题意可得a=2，c=1，由a，b，c的关系可得b，进而得到椭圆方程；（Ⅱ）设直线AE的方程为y=k（x﹣2），代入椭圆方程，运用韦达定理，可得E的坐标，由两直线垂直可得F的坐标，再由直线的斜率公式，结合基本不等式即可得到斜率的最值，进而得到所求范围．
练习册系列答案
相关题目
