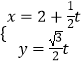Question

【题目】已知 ．
（1）求f（x）的周期及其图象的对称中心；
（2）△ABC中，角A、B、C所对的边分别是a、b、c，满足（2a﹣c）cosB=bcosC，求f（B）的值．

Answer 1

【答案】
（1）解：∵已知 = sin + cos +1=sin（ + ）+1，

故f（x）的周期为 =4π．

由sin（ + ）=0 求得 + =kπ，k∈z，即 x=2kπ﹣ ，故函数的图象的对称中心为（2kπ﹣ ，0）

（2）解：△ABC中，∵（2a﹣c）cosB=bcosC，由正弦定理可得 （2sinA﹣sinC）cosB=sinBcosC，

化简可得2sinAcosB=sin（B+C）=sinA，∴cosB= ，∴B= ．

∴f（B）=sin（ + ）+1= +1

【解析】（1）利用两角和差的正弦公式、二倍角公式化简函数f（x）的解析式为sin（ + ）+1，由此可得f（x）的周期及其图象的对称中心．（2）△ABC中，由（2a﹣c）cosB=bcosC，利用正弦定理化简可得得2sinAcosB=sin（B+C）=sinA，故有cosB= ，由此求得 B 的值．
【考点精析】掌握两角和与差的正弦公式和二倍角的正弦公式是解答本题的根本，需要知道两角和与差的正弦公式：；二倍角的正弦公式：．