题目内容
【题目】设集合A={x|﹣1≤x≤2},B={x|x2﹣4x>0,x∈R},则A∩(RB)=( )
A.[1,2]
B.[0,2]
C.[1,4]
D.[0,4]
【答案】B
【解析】解:∵集合A={x|﹣1≤x≤2},B={x|x2﹣4x>0,x∈R}={x>4,或x<0},
∴ ![]() B={x|0≤x≤4},
B={x|0≤x≤4},
∴A∩(CRB)={x|0≤x≤2}.
故选B.
【考点精析】利用交、并、补集的混合运算对题目进行判断即可得到答案,需要熟知求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】为了丰富退休生活,老王坚持每天健步走,并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数(老王每天健步走的步数都在![]() 之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
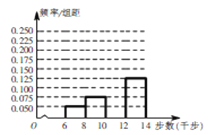
(1)完成频率分布直方图,并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替;
(2)某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天,求这2天的健步走结果属于同一评价级别的概率.
