题目内容
【题目】(本题满分12分)已知![]() ,函数
,函数![]()
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)若![]() ,求
,求![]() 在闭区间
在闭区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)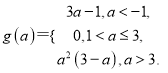 .
.
【解析】试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的极值和最值、利用导数求函数的切线方程等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,将![]() 代入
代入![]() 中,对
中,对![]() 求导,
求导, ![]() 为切点的纵坐标,而
为切点的纵坐标,而![]() 是切线的斜率,最后利用点斜式写出直线方程;第二问,对
是切线的斜率,最后利用点斜式写出直线方程;第二问,对![]() 求导,令
求导,令![]() ,将
,将![]() 分成两部分:
分成两部分: ![]() 和
和![]() 进行讨论,讨论函数的单调性,利用单调性判断函数的最小值,综合所有情况,得到
进行讨论,讨论函数的单调性,利用单调性判断函数的最小值,综合所有情况,得到![]() 的解析式.
的解析式.
试题解析:定义域: ![]() ,
, ![]()
(Ⅰ)当![]() 时,
时, ![]() ,则
,则![]()
![]() ,则
,则![]()
∴![]() 在
在![]() 处切线方程是:
处切线方程是: ![]() ,即
,即![]() ,
,
(Ⅱ)![]() ,令
,令![]() ,得到
,得到![]() ,
, ![]()
①当![]() 时,
时, ![]() ,则有
,则有
| 0 |
|
|
|
|
|
|
|
| 0 |
| 0 |
| ||
| 0 |
| 极大 |
| 极小 |
|
|
则最小值应该由![]() 与
与![]() 中产生,
中产生,
当![]() 时,
时, ![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,此时
,此时![]() ,
,
②当![]() 时,
时, ![]() ,则有
,则有
| 0 |
|
|
|
|
|
| 0 |
| ||
| 0 |
| 极小 |
|
|
则![]() ,
,
综上所述:当![]() 时,
时, ![]() 在区间
在区间![]() 上的最小值
上的最小值

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示. 
(1)下表是年龄的频数分布表,求正整数a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
