题目内容
【题目】一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
【答案】设该农民种![]() 亩水稻,
亩水稻, ![]() 亩花生时,能获得利润
亩花生时,能获得利润![]() 元.则
元.则
![]()
即![]() ………………2分
………………2分
 即
即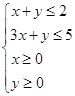 ………………4分
………………4分
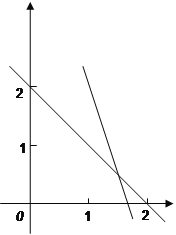
作出可行域如图阴影部分所示, ………………8分
作出基准直线![]() ,在可行域内平移直线
,在可行域内平移直线![]() ,可知当直线过点
,可知当直线过点![]() 时,纵截距
时,纵截距![]() 有最大值,…………………………10分
有最大值,…………………………10分
由![]() 解得
解得![]() ,…………………………12分
,…………………………12分
故当![]() ,
, ![]() 时,
时, ![]() 元,…………………………13分
元,…………………………13分
答:该农民种![]() 亩水稻,
亩水稻, ![]() 亩花生时,能获得最大利润,最大利润为1650元
亩花生时,能获得最大利润,最大利润为1650元
【解析】试题分析:设出玉米和花生种植的亩数分别为x,y,则依题意得,收益z=960x+420y,同时列出x,y满足的不等式组,利用线性规划求出最大值即可。
试题解析:设该农民种![]() 亩玉米,
亩玉米, ![]() 亩花生时,能获得利润
亩花生时,能获得利润![]() 元。
元。
则![]()
 即
即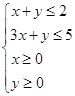
作出可行域如图所示,
故当![]() ,
, ![]() 时,
时, ![]() 元
元
答:该农民种![]() 亩玉米,
亩玉米, ![]() 亩花生时,能获得最大利润,最大利润为1650元。
亩花生时,能获得最大利润,最大利润为1650元。

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示. 
(1)下表是年龄的频数分布表,求正整数a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.