题目内容
【题目】已知直线l1经过点A（﹣3，0），B（3，2），直线l2经过点B，且l1⊥l2 ．
（1）求经过点B且在两坐标轴上的截距相等的直线的方程；
（2）设直线l2与直线y=8x的交点为C，求△ABC外接圆的方程．
【答案】
（1）解：设经过点B且在两坐标轴上的截距相等的直线为m，
①当直线m经过原点时，在两坐标轴上的截距都为零，符合题意．
此时，直线m的方程为y= 
x；
②当直线m不经过原点时，设方程为 
，
将点B（3，2）代入，得 
，解之得a=5，
此时直线m的方程为 
，化简得x+y﹣5=0．
综上所述，直线m方程为y= x或x+y﹣5=0，即为所求直线的方程
（2）解：∵直线l1经过点A（﹣3，0），B（3，2），
∴直线l1的斜率k1= 
= 
，
∵l1⊥l2，∴直线l2的斜率k2= 
=﹣3．
又∵直线l2经过点B（3，2），
∴直线l2的方程为y﹣2=﹣3（x﹣3），即y=﹣3x+11，
由 
联解，得 
，可得直线l2与直线y=8x的交点为C（1，8）．
设经过A、B、C三点的圆方程为x2+y2+Dx+Ey+F=0，
可得 
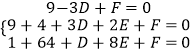，解之得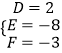 
，
∴经过A、B、C三点的圆方程为x2+y2+2x﹣8y﹣3=0，即为△ABC外接圆的方程
【解析】（1）根据直线经过原点或不经过原点，分两种情况加以讨论，利用直线在坐标轴上截距的概念和直线方程的截距式，即可算出满足条件的直线方程；（2）由A、B的坐标算出直线l1的斜率k1= ，从而得到l2的斜率k2= =﹣3，利用点斜式列式可得直线l2的方程为y=﹣3x+11．联解直线l2与直线y=8x，算出交点为C（1，8），设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0，代入A、B、C的坐标解出D、E、F的值，即可得到所求△ABC外接圆的方程．
【考点精析】解答此题的关键在于理解截距式方程的相关知识，掌握直线的截距式方程：已知直线
与
轴的交点为A
，与
轴的交点为B
，其中
，以及对圆的标准方程的理解，了解圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程．
