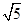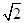题目内容
已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为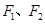 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为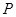 ,
,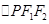 是以
是以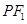 为底边的等腰三角形,若
为底边的等腰三角形,若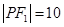 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为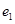 ,
,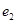 ,则
,则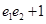 的取值范围是( )
的取值范围是( )
A.(1,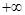 ) ) | B.( , ,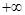 ) ) | C.(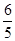 , ,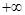 ) ) | D.(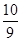 ,+ ,+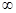 ) ) |
B
解析试题分析:设椭圆与双曲线的半焦距为c,PF1=r1,PF2=r2.
由题意知r1=10,r2=2c,且r1>r2,2r2>r1,∴2c<10,2c+2c>10,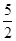 <c<5,
<c<5,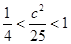 。
。
∴e2=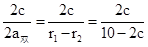 =
=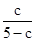 ;
;
e1=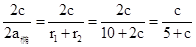 .
.
∴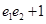 =
=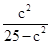 +1=
+1=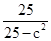 =
=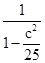 >
> ,故选B。
,故选B。
考点:本题主要考查椭圆、双曲线的几何性质,不等式的性质。
点评:中档题,首先结合图形分析,确定得到几何量之间的关系,进一步确定c的范围。确定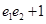 的范围过程中,利用了不等式的性质。
的范围过程中,利用了不等式的性质。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当 为等边三角形时,其面积为
为等边三角形时,其面积为
A. | B.4 | C.6 | D.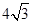 |
设 、
、 是双曲线
是双曲线 的左、右两个焦点,若双曲线右支上存在一点P,使
的左、右两个焦点,若双曲线右支上存在一点P,使 ,且
,且 ,则
,则 的值为( )
的值为( )
| A.2 | B. | C.3 | D. |
抛物线 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为
A. | B. | C. | D. |
过双曲线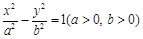 左焦点
左焦点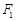 的直线与以右焦点
的直线与以右焦点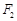 为圆心、
为圆心、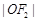 为半径的圆相切于A点,且
为半径的圆相切于A点,且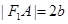 ,则双曲线的离心率为
,则双曲线的离心率为
A.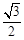 | B.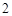 | C.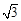 | D.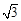 |
设 、
、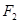 分别是椭圆
分别是椭圆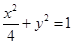 的左、右焦点,
的左、右焦点, 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且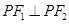 ,则点
,则点 的横坐标为
的横坐标为
A.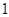 | B.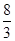 | C.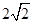 | D.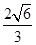 |
 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x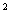 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ). 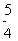
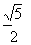
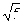
 (
(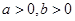 )的右焦点
)的右焦点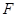 作圆
作圆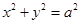 的切线
的切线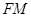 ,交
,交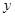 轴于点
轴于点 ,切圆于点
,切圆于点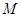 ,若
,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )