题目内容
抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当 为等边三角形时,其面积为
为等边三角形时,其面积为
A. | B.4 | C.6 | D.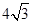 |
D
解析试题分析:据题意知,△PMF为等边三角形,PF=PM,
∴PM⊥抛物线的准线,设P(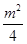 ,m),则M(-1,m),
,m),则M(-1,m),
等边三角形边长为1+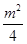 ,F(1,0),
,F(1,0),
所以,由PM=FM,得1+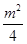 =
=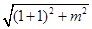 ,解得m=2
,解得m=2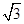 ,
,
∴等边三角形边长为4,其面积为4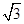 ,
,
故选D.
考点:抛物线的几何性质,直线与抛物线的位置关系。
点评:中档题,结合抛物线及其准线,应用抛物线的几何性质,明确三角形特征,建立假设量的方程,进一步计算三角形面积。

练习册系列答案
相关题目
如图,F1,F2是双曲线C: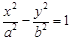 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与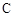 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
A.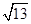 | B.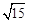 |
| C.2 | D.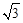 |
若点O和点F分别为椭圆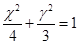 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则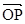 ·
·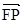 的最大值为( ).
的最大值为( ).
| A.2 | B.3 | C.6 | D.8 |
已知双曲线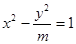 的虚轴长是实轴长的2倍,则实数
的虚轴长是实轴长的2倍,则实数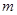 的值是( )
的值是( )
A.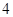 | B.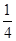 | C.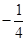 | D.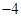 |
已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为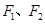 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为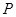 ,
,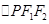 是以
是以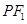 为底边的等腰三角形,若
为底边的等腰三角形,若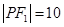 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为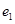 ,
,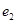 ,则
,则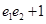 的取值范围是( )
的取值范围是( )
A.(1,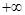 ) ) | B.( , ,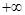 ) ) | C.(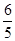 , ,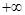 ) ) | D.(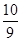 ,+ ,+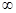 ) ) |
设抛物线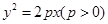 的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为
的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为
A.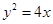 或 或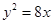 | B.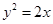 或 或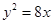 |
C.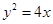 或 或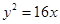 | D.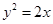 或 或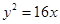 |
 ,
,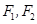 为其两个焦点,点
为其两个焦点,点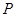 为双曲线上一点,若
为双曲线上一点,若 ,则
,则 的值为________.
的值为________.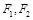 为椭圆
为椭圆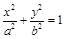 (
(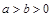 )的两个焦点,过F2作椭圆的弦AB,若
)的两个焦点,过F2作椭圆的弦AB,若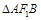 的周长为16,椭圆的离心率
的周长为16,椭圆的离心率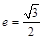 ,则椭圆的方程为( )
,则椭圆的方程为( )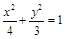
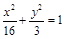
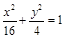
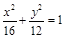
 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( ) 


