Question

【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》，某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查（调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程）．本次调查结果如下．图中，课程A，B，C，D，E为人文类课程，课程F，G，H为自然科学类课程．为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组（以下简称“组M”）．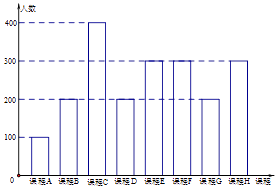
（Ⅰ）在“组M”中，选择人文类课程和自然科学类课程的人数各有多少？
（Ⅱ）某地举办自然科学营活动，学校要求：参加活动的学生只能是“组M”中选择F课程或G课程的同学，并且这些同学以自愿报名缴费的方式参加活动．选择F课程的学生中有x人参加科学营活动，每人需缴纳2000元，选择G课程的学生中有y人参加该活动，每人需缴纳1000元．记选择F课程和G课程的学生自愿报名人数的情况为（x，y），参加活动的学生缴纳费用总和为S元．
（ⅰ）当S=4000时，写出（x，y）的所有可能取值；
（ⅱ）若选择G课程的同学都参加科学营活动，求S＞4500元的概率．

Answer 1

【答案】解：（Ⅰ）选择人文类课程的人数为（100+200+400+200+300）×1%=12（人），

选择自然科学类课程的人数为（300+200+300）×1%=8（人）．

（Ⅱ）（ⅰ）当缴纳费用S=4000时，（x，y）只有两种取值情况：（2，0），（1，2）；

（ⅱ）设事件A：若选择G课程的同学都参加科学营活动，缴纳费用总和S超过4500元．

在“组M”中，选择F课程和G课程的人数分别为3人和2人．

由于选择G课程的两名同学都参加，下面考虑选择F课程的3位同学参加活动的情况．

设每名同学报名参加活动用a表示，不参加活动用b表示，

则3名同学报名参加活动的情况共有以下8种情况：aaa，aab，aba，baa，bba，bab，abb，bbb．

当缴纳费用总和S超过4500元时，选择F课程的同学至少要有2名同学参加，有如下4种：aaa，aab，aba，baa．

所以，S＞4500元的概率

【解析】（Ⅰ）利用频率分布直方图能求出选择人文类课程的人数和选择自然科学类课程的人数．（Ⅱ）（ⅰ）当缴纳费用S=4000时，利用列举法能求出（x，y）的不同的取值情况．（ⅱ）设事件A：若选择G课程的同学都参加科学营活动，缴纳费用总和S超过4500元．在“组M”中，选择F课程和G课程的人数分别为3人和2人．由于选择G课程的两名同学都参加，下面考虑选择F课程的3位同学参加活动的情况．设每名同学报名参加活动用a表示，不参加活动用b表示，利用列举法能求出S＞4500元的概率．
【考点精析】本题主要考查了频率分布直方图的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息才能正确解答此题．