题目内容
【题目】已知函数f(x)=lnx﹣x+m(m∈R)的图象与x轴相交于A(x1 , 0),B(x2 , 0)两点,且x1<x2 .
(I)若函数f(x)的最大值为2,求m的值;
(Ⅱ)若 ![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(Ⅲ)证明:x1x2<1.
【答案】解:(Ⅰ)∵f(x)=lnx﹣x+m,
∴f′(x)= ![]() ﹣1=
﹣1= ![]()
当x>1时,f′(x)<0,函数f(x)单调递减,
当0<x<1时,f′(x)>0,函数f(x)单调递增,
∴f(x)max=f(1)=ln1﹣1+m=2,
解得m=3,
(Ⅱ)当x>1时,f(x)<k(1﹣ ![]() )+xf′(x)+m﹣2,(k≤2)恒成立,
)+xf′(x)+m﹣2,(k≤2)恒成立,
∴lnx﹣x+m<k(1﹣ ![]() )+1﹣x+m﹣2恒成立,
)+1﹣x+m﹣2恒成立,
∴(lnx+1)>k(x﹣3),k≤2,(*)
∵当x>1时,(*)恒成立,
当x>1时,(lnx+1)﹣k(x﹣3)>0恒成立,
令g(x)=(lnx+1)﹣k(x﹣3),
∴g′(x)=lnx+2﹣k,
∵x>1,k≤2,
∴g′(x)>0,
∴g(x)在(1,+∞)单调递增,
∴g(x)>g(1)=1+2k>0,
∴k>﹣ ![]() ,
,
即k的取值范围为(﹣ ![]() ,2];
,2];
(Ⅲ)函数f(x)=lnx﹣x+m(m∈R)的图象与x轴相交于A(x1,0),B(x2,0)两点,且x1<x2.
结合(Ⅰ)可得x1∈(0,1),x2∈(1,+∞),
∴ ![]() ∈(0,1),
∈(0,1),
∵f(x1)=f(x2),
∴lnx1﹣x1=lnx2﹣x2,
∴f(x1)﹣f( ![]() )=lnx1﹣x1+lnx2+
)=lnx1﹣x1+lnx2+ ![]() =lnx2﹣x2+lnx2+
=lnx2﹣x2+lnx2+ ![]() =2lnx2﹣x2+
=2lnx2﹣x2+ ![]() ,
,
令h(x)=2lnx﹣x+ ![]() ,x>1,
,x>1,
∴h′(x)= ![]() ﹣1﹣
﹣1﹣ ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() <0,
<0,
∴h(x)在(1,+∞)上单调递减,
∴h(x)<h(1)=0,
∴f(x1)﹣f( ![]() )<0,
)<0,
∴f(x1)<f( ![]() ),
),
∵函数f(x)在(0,1)上单调递增,
∴x1< ![]() ,
,
∴x1x2<1
【解析】(1)利用导数讨论函数f(x)的单调性,从而求出f(x)的最大值;(2)构造函数g(x)=(lnx+1)-k(x-3),利用导数讨论g(x)在(1,+![]() )内的单调性;(3)结合(1)确定x1、x2的取值范围,根据f(x1)=f(x2)找出x1与x2之间的关系,构造函数h(x)=2lnx-x+
)内的单调性;(3)结合(1)确定x1、x2的取值范围,根据f(x1)=f(x2)找出x1与x2之间的关系,构造函数h(x)=2lnx-x+![]() ,利用导数讨论函数h(x)在(1,+
,利用导数讨论函数h(x)在(1,+![]() )内的单调性.
)内的单调性.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表: 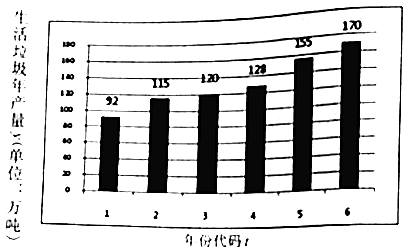
2016年初 | 2016年末 | |
社区A | 539 | 568 |
社区B | 543 | 585 |
社区C | 568 | 600 |
社区D | 496 | 513 |
注1:年份代码1~6分别对应年份2011~2016
注2:参与度= ![]() ×100%
×100%
参与度的年增加值=年末参与度﹣年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为 ![]() =14.8t+
=14.8t+ ![]() ,预测2020年该年生活垃圾的产生量;
,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题: ①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?