Question

【题目】已知椭圆C：x2+4y2=4．
（1）求椭圆C的离心率；
（2）椭圆C的长轴的两个端点分别为A，B，点P在直线x=1上运动，直线PA，PB分别与椭圆C相交于M，N两个不同的点，求证：直线MN与x轴的交点为定点．

Answer 1

【答案】
（1）解：由椭圆的标准方程： ，

则a=2，b=1，则c= ，

∴椭圆的离心率e= =

（2）证明：∵椭圆C的左，右顶点分别为A，B，点P是直线x=1上的动点，

∴A（﹣2，0），B（2，0），设P（1，t），

则kPA= = ，直线PA：y= （x+2），

联立得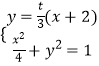： 整理，得（4t2+9）x2+16t2x+16t2﹣36=0，

﹣2xM= ，则xM= ，yM= （xM+2）= ，

则M（ ， ），

同理得到N（ ， ）

由椭圆的对称性可知这样的定点在x轴，

不妨设这个定点为Q（m，0），

又kM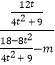Q= ，kNQ= ，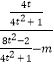

∵kMQ=kNQ，

∴（8m﹣32）t2﹣6m+24=0，m=4．

∴直线MN经过一定点Q（4，0），

直线MN与x轴的交点为定点Q（4，0）．

【解析】（1）求得椭圆的标准方程，则a=2，b=1，则c= ，利用椭圆的离心率公式，即可求得椭圆C的离心率；（2）设P（1，t），由已知条件分别求出M，N的坐标，设定点为Q，再由kMQ=kNQ，能证明直线MN经过一定点Q（4，0）．