题目内容
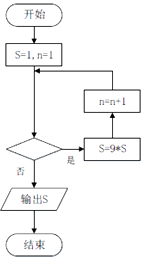
【题目】已知函数 ![]() ,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
(Ⅱ)若f(x)存在极小值和极大值,证明:f(x)的极小值大于极大值.
【答案】解:(Ⅰ)函数f(x)的定义域是{x|x>0,且x≠2},
f′(x)=﹣ ![]() +
+ ![]() =
= ![]() .
.
令f′(x)=0得x2﹣(4+a)x+4=0.
若曲线y=f(x)存在斜率为0的切线,则方程x2﹣(4+a)x+4=0在定义域{x|x>0,且x≠2}上有解,
不妨设x=1是方程x2﹣(4+a)x+4=0的解,则a=1.
∴当a=1时,曲线y=f(x)存在斜率为0的切线.
(Ⅱ)由(Ⅰ)得 f′(x)=﹣ ![]() +
+ ![]() .
.
①当a≤0时,f′(x)>0恒成立,
∴f(x)在区间(0,2)和(2,+∞)上单调递增,不合题意.
②当a>0时,令f′(x)=0,得x2﹣(4+a)x+4=0.
△=(4+a)2﹣16=a2+8a>0,
∴方程必有两个不相等的实数解x1,x2,不妨设x1<x2.
则 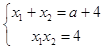 ,∴0<x1<2<x2.
,∴0<x1<2<x2.
列表:
x | (0,x1) | x1 | (x1,2) | (2,x2) | x2 | (x2,+∞) |
f′(x) | + | 0 | ﹣ | ﹣ | 0 | + |
f(x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
∴f(x)存在极大值f(x1),极小值f(x2).
f(x2)﹣f(x1)=( ![]() +lnx2)﹣(
+lnx2)﹣( ![]() +lnx1)=a(
+lnx1)=a( ![]() )+(lnx2﹣lnx1).
)+(lnx2﹣lnx1).
∵0<x1<2<x2,且a>0,
∴a( ![]() )>0,lnx2﹣lnx1>0,
)>0,lnx2﹣lnx1>0,
∴f(x2)>f(x1).
∴f(x)的极小值大于极大值
【解析】(I)令f′(x)=0在定义域上有解即可;(II)判断f(x)的单调性,求出f(x)的极值,再利用作差法计算极值的差即可.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表: 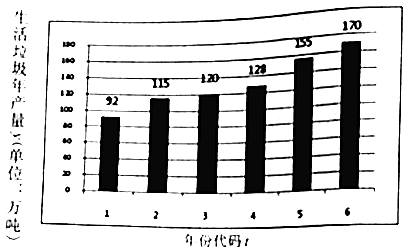
2016年初 | 2016年末 | |
社区A | 539 | 568 |
社区B | 543 | 585 |
社区C | 568 | 600 |
社区D | 496 | 513 |
注1:年份代码1~6分别对应年份2011~2016
注2:参与度= ![]() ×100%
×100%
参与度的年增加值=年末参与度﹣年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为 ![]() =14.8t+
=14.8t+ ![]() ,预测2020年该年生活垃圾的产生量;
,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题: ①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?