题目内容
(本小题满分13分)椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为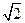 、离心率为
、离心率为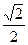 ,直线
,直线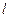 与y轴交于点P(0,
与y轴交于点P(0,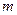 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且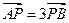 。
。
(I)求椭圆方程;
(II)求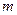 的取值范围。
的取值范围。
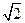 、离心率为
、离心率为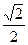 ,直线
,直线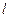 与y轴交于点P(0,
与y轴交于点P(0,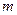 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且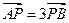 。
。(I)求椭圆方程;
(II)求
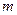 的取值范围。
的取值范围。解:(I)设C: 设
设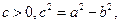
由条件知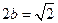 ,
,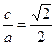 ,
,
∴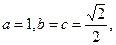 …………3分
…………3分
故C的方程为: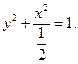 …………5分
…………5分
(II)设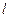 与椭圆C交点为A(
与椭圆C交点为A(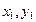 ),B(
),B(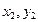 )
)
由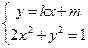 得
得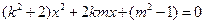
得(k2+2)x2+2kmx+(m2-1)=0
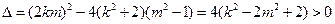 (*)
(*)
 …………8分
…………8分
∵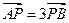 ∴
∴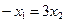 ∴
∴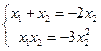
消去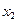 ,得
,得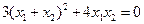 ,∴
,∴
整理得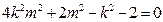
 …………10分
…………10分
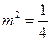 时,上式不成立;
时,上式不成立; 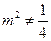 时,
时,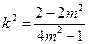 ,
,
由(*)式得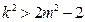
因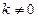 ∴
∴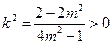 ,∴
,∴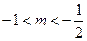 或
或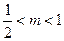
即所求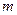 的取值范围为
的取值范围为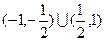 …………13分
…………13分
 设
设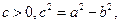
由条件知
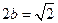 ,
,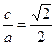 ,
,∴
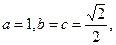 …………3分
…………3分故C的方程为:
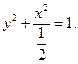 …………5分
…………5分(II)设
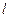 与椭圆C交点为A(
与椭圆C交点为A(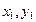 ),B(
),B(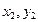 )
)由
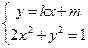 得
得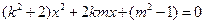
得(k2+2)x2+2kmx+(m2-1)=0
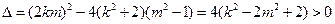 (*)
(*) …………8分
…………8分∵
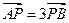 ∴
∴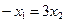 ∴
∴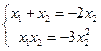
消去
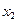 ,得
,得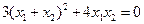 ,∴
,∴
整理得
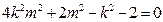
 …………10分
…………10分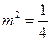 时,上式不成立;
时,上式不成立; 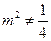 时,
时,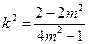 ,
,由(*)式得
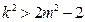
因
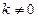 ∴
∴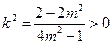 ,∴
,∴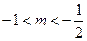 或
或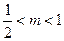
即所求
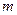 的取值范围为
的取值范围为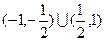 …………13分
…………13分略

练习册系列答案
相关题目
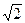 ),且离心率e满足:
),且离心率e满足: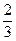 ,e,
,e,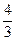 成等比数列.
成等比数列.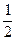
 求出l的倾斜角的范围;若不存在,请说明理由.
求出l的倾斜角的范围;若不存在,请说明理由.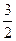 ),两个焦
),两个焦 点为(-1,0)、(1,0)。
点为(-1,0)、(1,0)。 满分12
满分12 分)
分)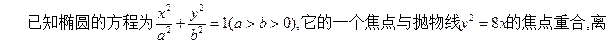
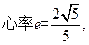 过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点.
过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点. 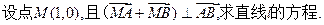
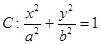 的左焦点作直线
的左焦点作直线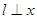 轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )
轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )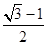
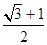
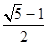
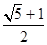
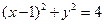 与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.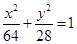 ,点
,点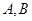 是它的两个焦点.当静止的小球从点
是它的两个焦点.当静止的小球从点 开始出发,沿直线运动,经椭圆壁反射后再回到点
开始出发,沿直线运动,经椭圆壁反射后再回到点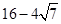
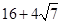 或28或
或28或
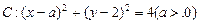 及直线l:x-y+3=O,当直线l被圆C截得的
及直线l:x-y+3=O,当直线l被圆C截得的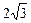 时,则a=( )
时,则a=( )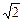
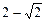
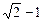
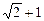
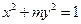 的离心率为
的离心率为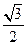 ,则它的长半轴长为_______________
,则它的长半轴长为_______________