题目内容
(本小题满分13分)已知椭圆的中心在原点,一个焦点F1(0,-2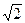 ),且离心率e满足:
),且离心率e满足: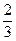 ,e,
,e,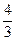 成等比数列.
成等比数列.
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=-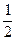
平分.若存在, 求出l的倾斜角的范围;若不存在,请说明理由.
求出l的倾斜角的范围;若不存在,请说明理由.
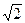 ),且离心率e满足:
),且离心率e满足: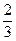 ,e,
,e,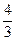 成等比数列.
成等比数列.(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=-
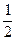
平分.若存在,
 求出l的倾斜角的范围;若不存在,请说明理由.
求出l的倾斜角的范围;若不存在,请说明理由.解:(1)依题意e=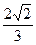 .
.
又F1(0,-2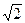 ), c=2
), c=2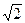 ,a=3,b=1,∴所求方程为x2+
,a=3,b=1,∴所求方程为x2+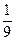 y2=1
y2=1
(2)假设存在直线l,依题意l交椭圆所得弦MN被x=-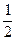 平分,∴直线l的斜率
平分,∴直线l的斜率
存在.设直线l:y=kx+m
由 消去y,整理得
消去y,整理得
(k2+9)x2+2k mx+m2-9=0
mx+m2-9=0
∵l与椭圆交于不同的两点M,N,
∴Δ=4k2m2-4(k2+9)(m2-9)>0
即m2-k2-9<0 ①
设M(x1,y1),N(x2,y2)
∴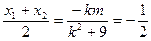 ,
,
∴m=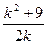 ②
②
把②代入①式中得
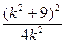 -(k2+9)<0
-(k2+9)<0
∴k>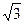 或k<-
或k<-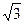
∴直线l倾斜角α∈(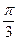 ,
,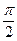 )∪(
)∪(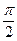 ,
,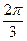 )
)
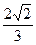 .
.又F1(0,-2
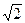 ), c=2
), c=2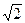 ,a=3,b=1,∴所求方程为x2+
,a=3,b=1,∴所求方程为x2+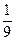 y2=1
y2=1(2)假设存在直线l,依题意l交椭圆所得弦MN被x=-
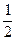 平分,∴直线l的斜率
平分,∴直线l的斜率存在.设直线l:y=kx+m
由
 消去y,整理得
消去y,整理得(k2+9)x2+2k
 mx+m2-9=0
mx+m2-9=0∵l与椭圆交于不同的两点M,N,
∴Δ=4k2m2-4(k2+9)(m2-9)>0
即m2-k2-9<0 ①
设M(x1,y1),N(x2,y2)
∴
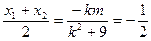 ,
,∴m=
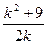 ②
②把②代入①式中得
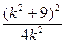 -(k2+9)<0
-(k2+9)<0∴k>
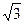 或k<-
或k<-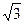
∴直线l倾斜角α∈(
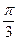 ,
,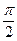 )∪(
)∪(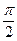 ,
,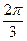 )
)略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
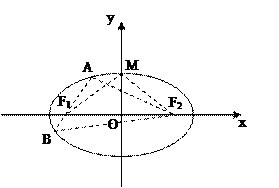
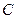 的中心在原点,焦点在
的中心在原点,焦点在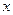 轴上,
轴上,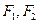 分别是椭圆
分别是椭圆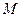 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过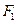 的直线
的直线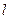 与椭圆交于
与椭圆交于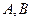 两点,
两点,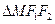 的面积为
的面积为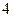 ,
,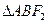 的周长为
的周长为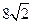 .
.
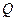 的坐标为
的坐标为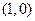 ,是否存在椭圆上的点
,是否存在椭圆上的点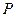 及以
及以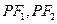 都相切,如存在,求出
都相切,如存在,求出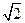 、离心率为
、离心率为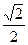 ,直线
,直线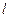 与y轴交于点P(0,
与y轴交于点P(0,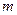 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且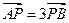 。
。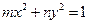 与直线
与直线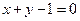 相交于
相交于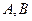 两点,过
两点,过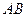 中点M与坐标原点的直线的斜率为
中点M与坐标原点的直线的斜率为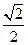 ,则
,则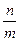 的值为( )
的值为( )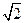
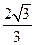
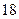 ,一个焦点的坐标是(3,0),则椭圆的标准方程为( )
,一个焦点的坐标是(3,0),则椭圆的标准方程为( )
 B
B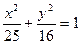 C
C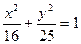 D
D
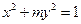 的离心率为
的离心率为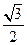 ,则
,则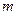 的值为 ( )
的值为 ( )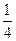
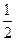
 双曲线
双曲线 抛物线
抛物线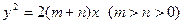 的离心率分别为
的离心率分别为 ,则
,则


 关系不确定
关系不确定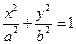 的焦点坐标为
的焦点坐标为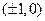 ,椭圆经过点
,椭圆经过点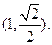
 上点N的直线交椭圆于点P,求
上点N的直线交椭圆于点P,求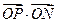 的值。
的值。 交椭圆于A、B两点,点
交椭圆于A、B两点,点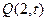 ,若
,若 的斜率无关,求t的值
的斜率无关,求t的值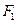 、
、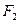 是椭圆
是椭圆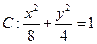 的焦点,在C上满足
的焦点,在C上满足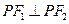 的点P的个数为
的点P的个数为