题目内容
已知椭圆C: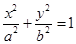
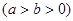 的离心率为
的离心率为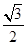 ,过右焦点
,过右焦点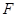 且斜率为
且斜率为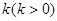 的直线与椭圆C相交于
的直线与椭圆C相交于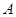 、
、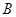 两点.若
两点.若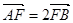 ,则
,则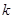 =( )
=( )
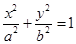
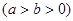 的离心率为
的离心率为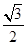 ,过右焦点
,过右焦点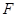 且斜率为
且斜率为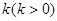 的直线与椭圆C相交于
的直线与椭圆C相交于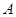 、
、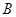 两点.若
两点.若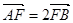 ,则
,则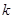 =( )
=( ) A.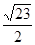 | B.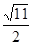 | C.2 | D.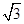 |
A

法一:如图BD=
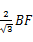 , AE=
, AE=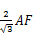 =
= 则AC=
则AC=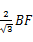 而AB=
而AB= K=tan
K=tan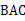 =
=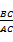 =
=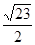
法二:设出A的坐标(m,n)根据
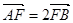 求出B的坐标
求出B的坐标然后A,B两点都在椭圆上,代入椭圆方程求出A,B的坐标,即可得斜率

练习册系列答案
相关题目
 )是椭圆E:
)是椭圆E: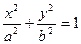 (
(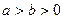 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.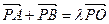 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;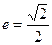 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为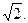
 且OP⊥OQ。试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由。
且OP⊥OQ。试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由。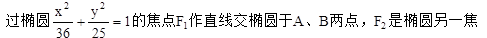 点,则△ABF2的周长是
点,则△ABF2的周长是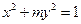 的离心率为
的离心率为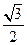 ,则
,则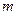 的值为 ( )
的值为 ( )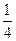
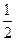
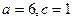 ,焦点在y轴上的椭圆的标准方程是
,焦点在y轴上的椭圆的标准方程是 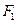 、
、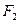 是椭圆
是椭圆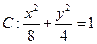 的焦点,在C上满足
的焦点,在C上满足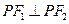 的点P的个数为
的点P的个数为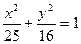 的离心率为
的离心率为 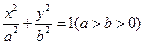 ,A(2,0)为椭圆与X轴的一个交点,过原点O的直线交椭圆于B、C两点,且
,A(2,0)为椭圆与X轴的一个交点,过原点O的直线交椭圆于B、C两点,且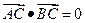 ,
,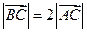
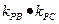 是否为定值?若是定值,求出该定值;若不是定值,请说明理由。
是否为定值?若是定值,求出该定值;若不是定值,请说明理由。