题目内容
(本小题满分14分)
已知椭圆中心在原点,焦点在x轴上,离心率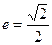 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为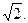
(1)求椭圆的标准方程;
(2)已知直线l与椭圆相交于P、Q两点,O为原点, 且OP⊥OQ。试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由。
且OP⊥OQ。试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由。
已知椭圆中心在原点,焦点在x轴上,离心率
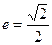 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为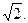
(1)求椭圆的标准方程;
(2)已知直线l与椭圆相交于P、Q两点,O为原点,
 且OP⊥OQ。试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由。
且OP⊥OQ。试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由。解:(1)设椭圆方程为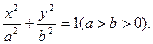 ………………1分
………………1分
因为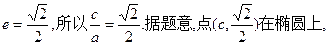
则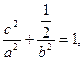
于是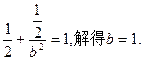 ………………4分
………………4分
因为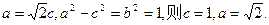 ………………5分
………………5分
故椭圆的方程为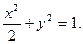 ………………6分
………………6分
(2)当直线l的斜率存在时,设直线l的方程为
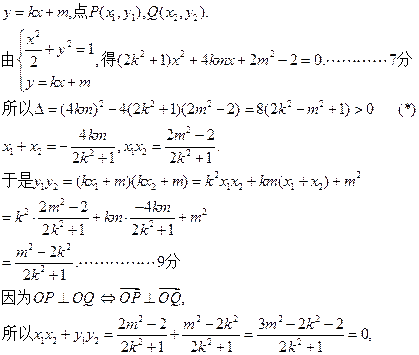
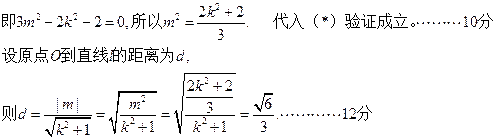
当直线l的斜率不存在时,因为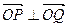 ,根据椭圆的对称性,不妨设直线OP、OQ的方程分别为
,根据椭圆的对称性,不妨设直线OP、OQ的方程分别为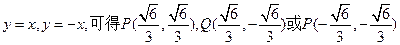 、
、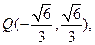
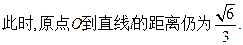 …………13分
…………13分
综上分析,点O到直线l的距离为定 值
值 …………14分
…………14分
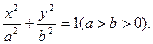 ………………1分
………………1分因为
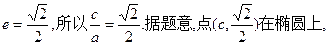
则
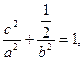
于是
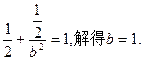 ………………4分
………………4分因为
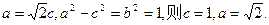 ………………5分
………………5分故椭圆的方程为
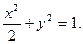 ………………6分
………………6分(2)当直线l的斜率存在时,设直线l的方程为
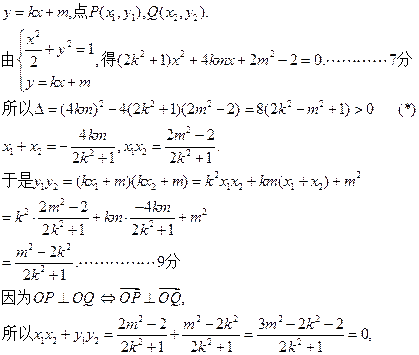
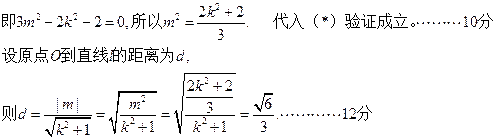
当直线l的斜率不存在时,因为
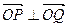 ,根据椭圆的对称性,不妨设直线OP、OQ的方程分别为
,根据椭圆的对称性,不妨设直线OP、OQ的方程分别为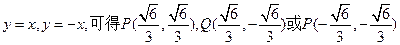 、
、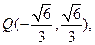
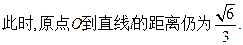 …………13分
…………13分综上分析,点O到直线l的距离为定
 值
值 …………14分
…………14分略

练习册系列答案
相关题目
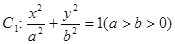 的左准线为
的左准线为 ,左右焦点分别为
,左右焦点分别为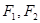 ,抛物线
,抛物线 的准线为
的准线为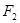 ,曲线
,曲线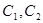 的一个交点为P,则
的一个交点为P,则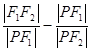 等于()
等于()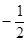 D
D 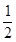
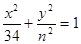 和双曲线
和双曲线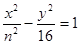 有相同的焦点,则实数
有相同的焦点,则实数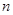 的值是( )
的值是( )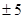 B
B 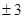 C 5 D 9
C 5 D 9
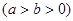 的离心率为
的离心率为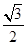 ,过右焦点
,过右焦点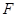 且斜率为
且斜率为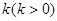 的直线与椭圆C相交于
的直线与椭圆C相交于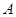 、
、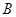 两点.若
两点.若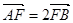 ,则
,则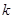 =( )
=( ) 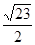
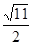
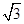
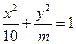 与双曲线
与双曲线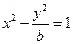 有相同的焦点,且椭圆与双曲线交于
有相同的焦点,且椭圆与双曲线交于 点
点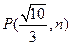 ,求椭圆及双曲线的方程.
,求椭圆及双曲线的方程.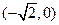 ,
,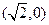 ,离心率是
,离心率是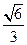 ,直线
,直线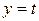 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。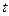 的值;
的值;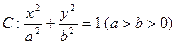 ,过右焦点
,过右焦点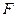 斜率为
斜率为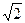 的直线与椭圆
的直线与椭圆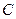 交于
交于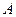 、
、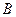 两
两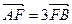 ,则椭圆
,则椭圆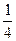

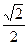
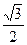
 果椭圆
果椭圆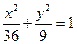 的弦被点(4,2)平分,则这条弦所在的直线方程是
的弦被点(4,2)平分,则这条弦所在的直线方程是 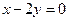
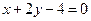
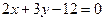
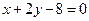
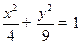 的上、下两个焦点分别为
的上、下两个焦点分别为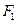 、
、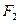 ,点
,点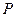 为该椭圆上一点,若
为该椭圆上一点,若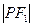 、
、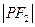 为方程
为方程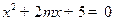 的两根,则
的两根,则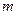 =" " .
=" " .